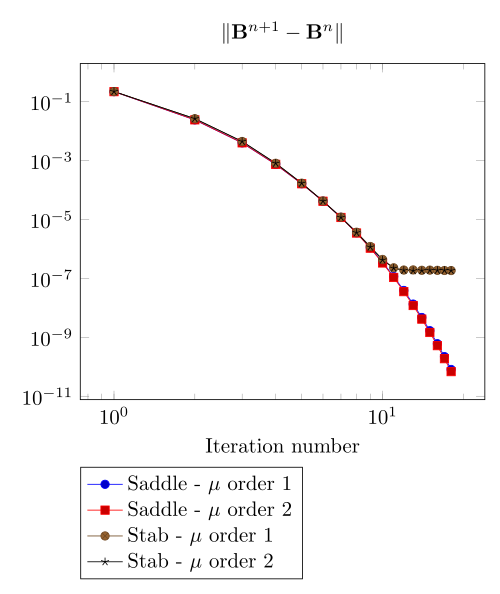
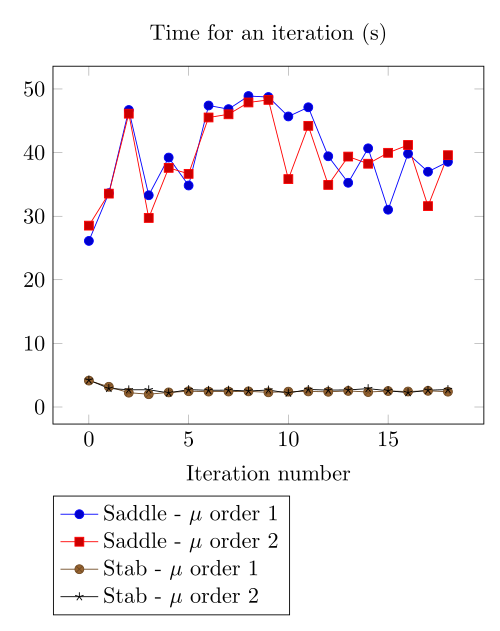
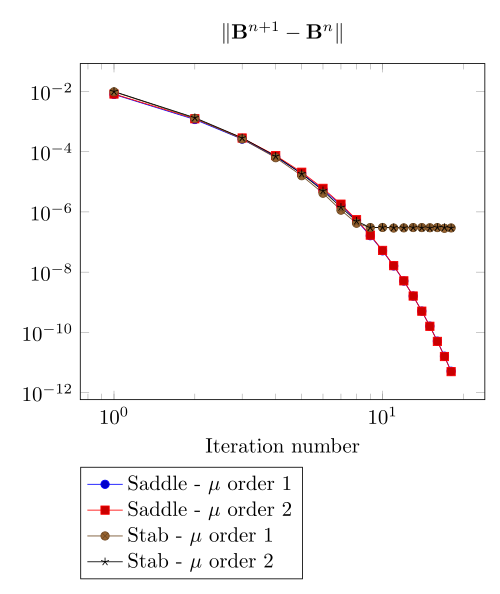
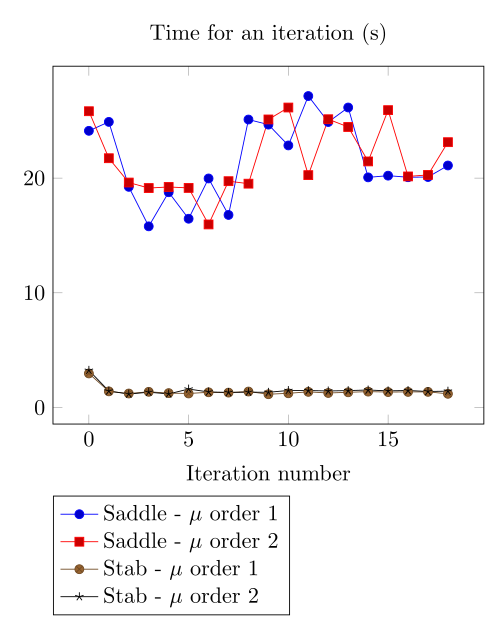
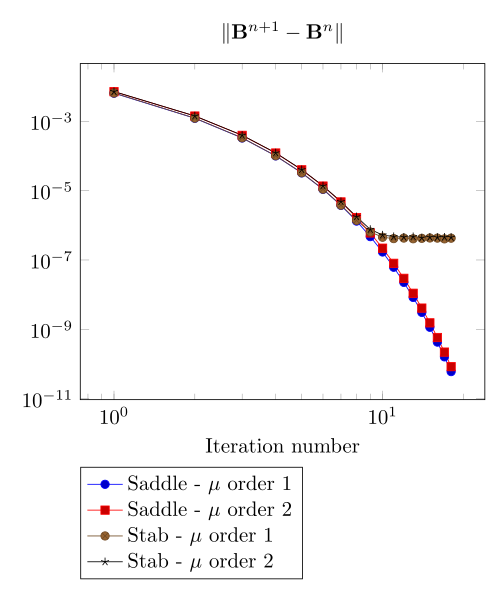
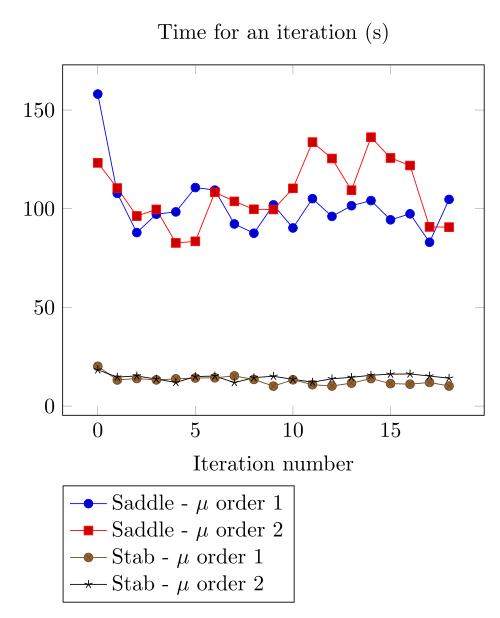
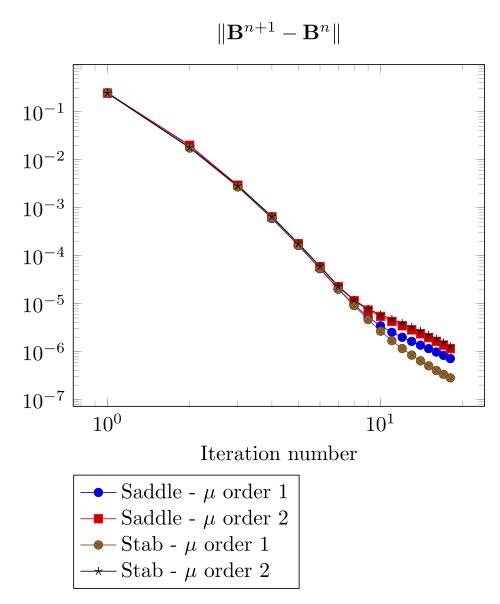
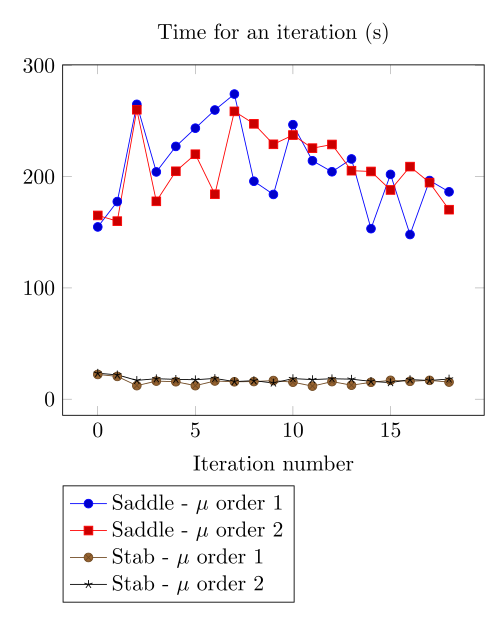
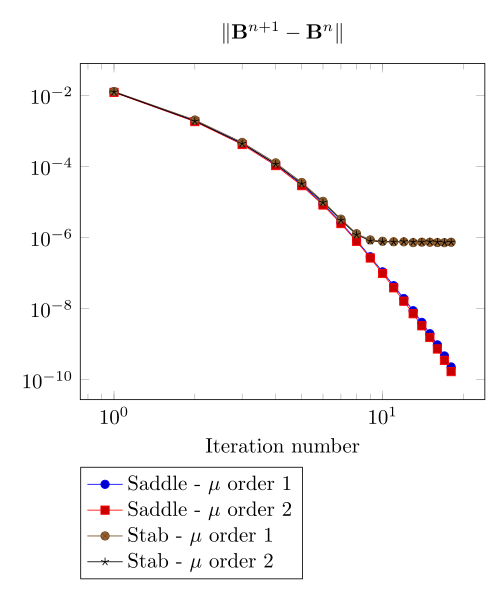
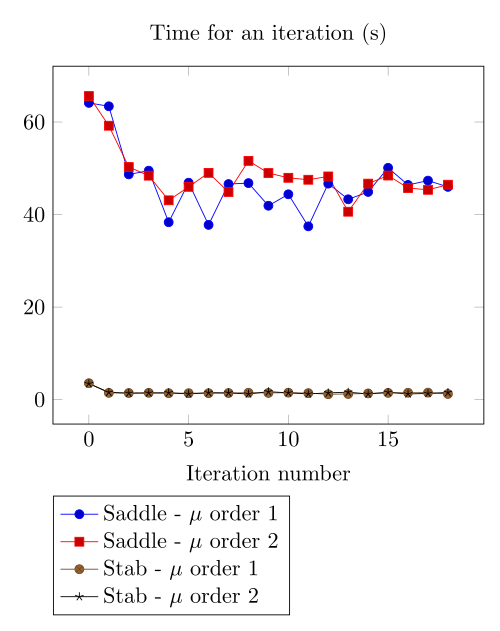
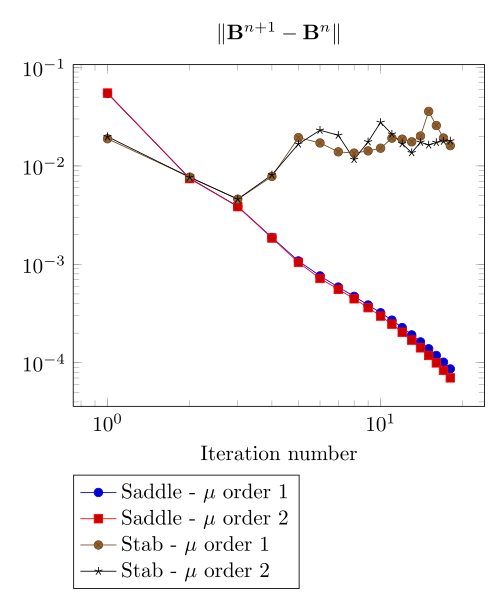
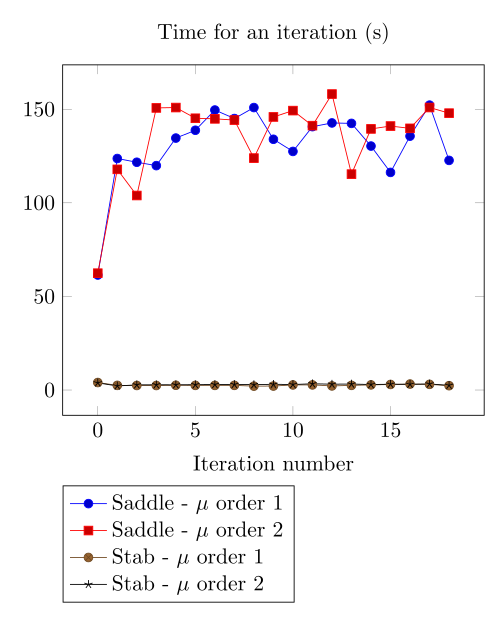
Team Workshop 13 Benchmark

The TEAM Workshop 13 benchmark aims to compare various formulations and implementations to solve the non linear magnetostatic problem. We reproduce that benchmark to evaluate the accuracy of our implementation.

1. Description

1.1. Geometry

The geometry consists on an exiting coil set between two steel channels which are not aligned together and a steel plate inserted inside the channels.

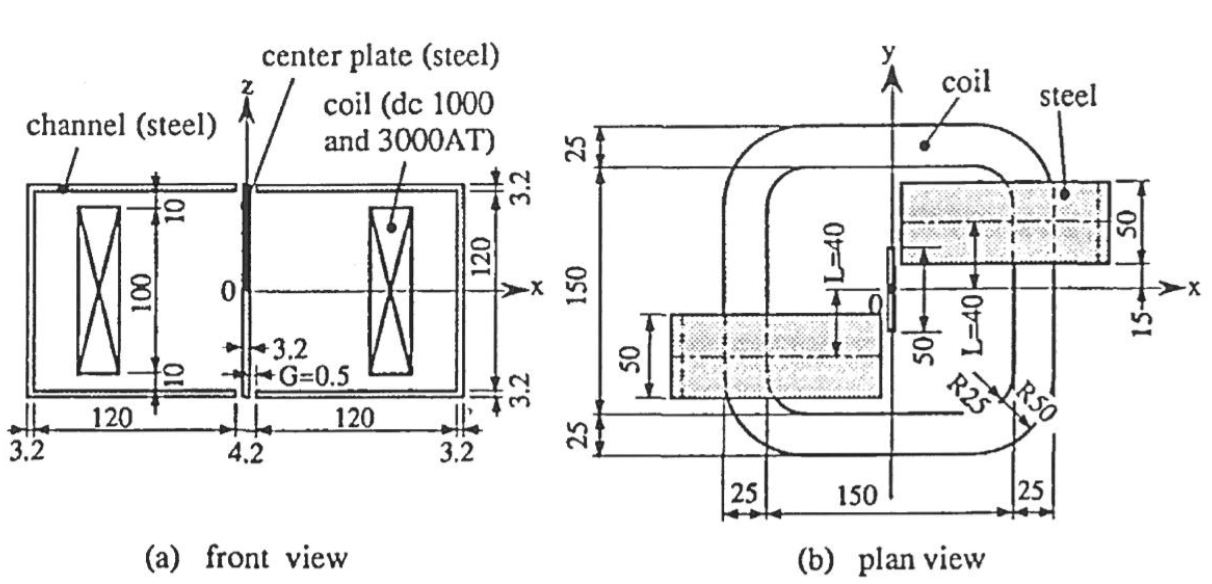
TWS Geometry
Figure 1: From cite bib Geometry

1.2. Magnetic permeability

We only process non linear problems.

To discriminate if the non linear law has an impact on the convergence, we run that benchmark with three \(B-H\) curves.

  • the one given by the Team Workshop 13 Benchmark,

  • the one given in GetDP,

  • a third one that is close to the two others, but with intermediate difficulty. We call it intermediate.

1.2.1. Interpolation

As long as we only process isotropic concretes, the non linear relations \(\mathbf{B} = \mathcal{B}(\mathbf{H})\) reads \(B = \mu(H) H \). It is that curve we have to interpolate. We propose piecewise linear interpolation and akima’s interpolation thanks to GSL.

The provided data are the relation of the magnetic induction amplitude \(B\) against the magnetic field magnitude \(H\).

We also tried the interpolation of \(\mu(H) H\) and \(\mu(H)\) directly. (idem for \(\nu\)).

Non Linear relation

We can observe the relation given in GetDP is the smoothest one. For the \(\Sigma-\Phi\) case, we only have one twist in the whole curve and the Team Workshop one provide two twists.

We use extrapolation to extend the magnetic permeability when \(\mathbf{H}\) goes to infinity.

2. Inputs

The source term - \(\mathbf{J}\) - is generated solving a Laplacian in each half coils. We present here a top view of an half of the coil.

half coil

The gradient of the solution of each problems is multiplied with the number of Ampère Turns we want.

\[\begin{aligned} -\Delta u &= 0\\ \left. u\right|_{\Gamma+} &= 1\\ \left. u\right|_{\Gamma-} &= 0\\ \mathbf{J} &= At \frac{\nabla u}{\|\nabla u \|} \end{aligned}\]

3. Outputs

We will compare the various fluxes the Team Workshop 13 Benchmark present and check the convergence in respect with various parameters:

  • the formulation: saddle or stabilized,

  • the current density

  • the non linear formulation

  • the \(\mu\) discretization (\(P_1\), \(P_2\)),

  • the non linear relation.

4. Behavior

Here are the meshes and spaces specifications

Number of elements

Number of Dof \(\mathbb{A}\)

Number of Dof \(p\)

Total

mesh 1

634 850

741 168

106 772

847 940

mesh 2

4 070 302

4 748 125

679 348

5 427 473

Every simulation has run over 48 processors on irma-atlas.

4.1. GetDP non linear curve

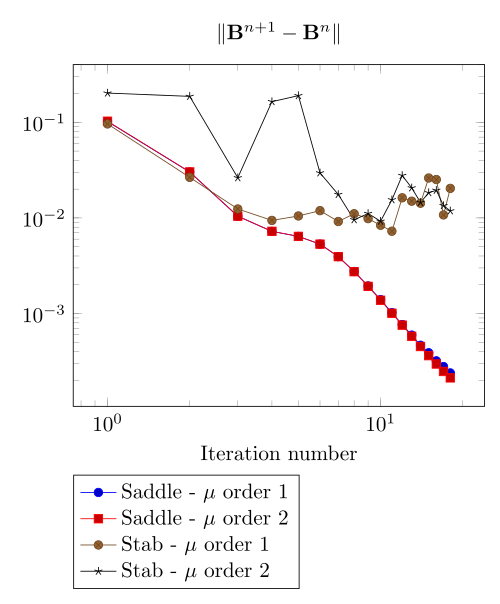
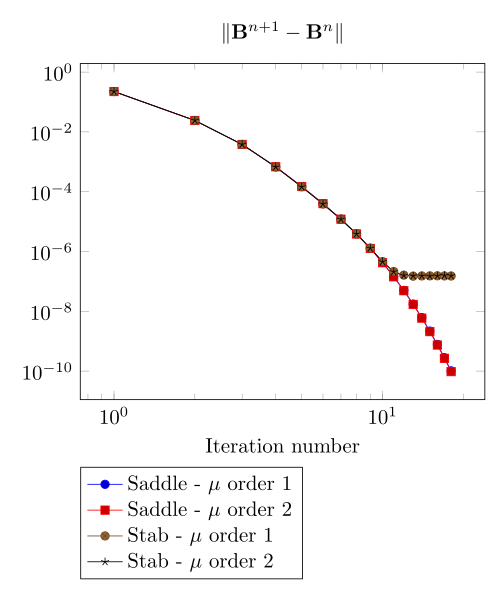
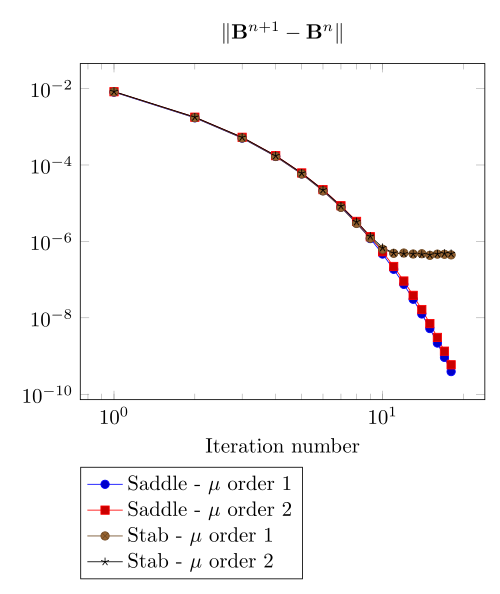
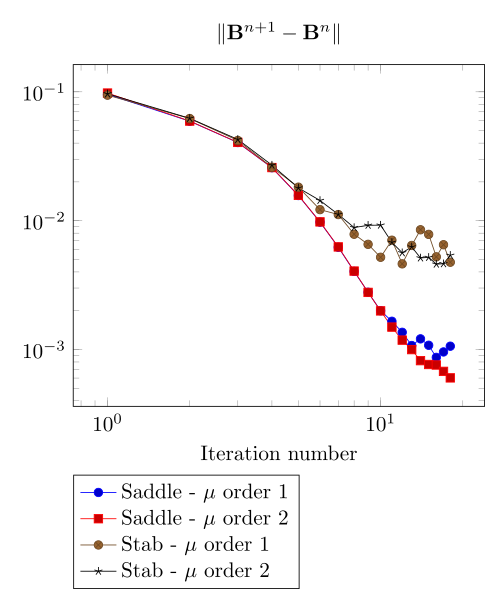
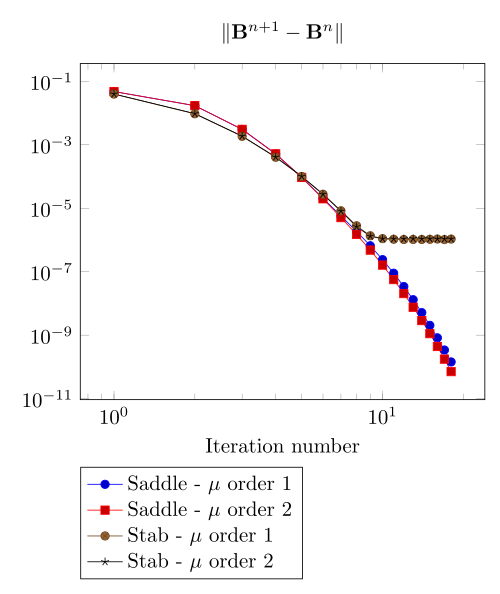
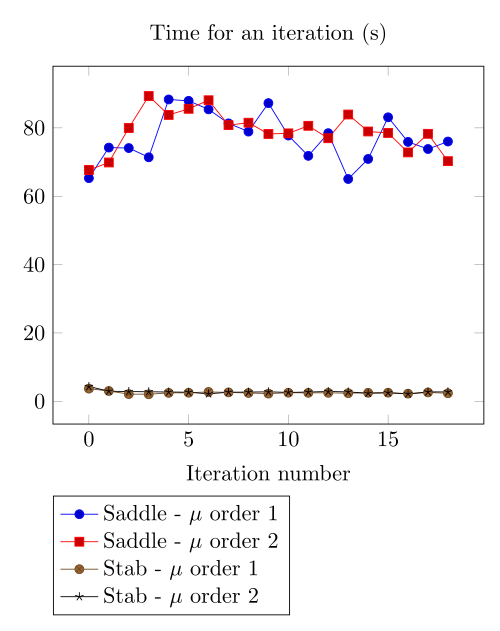
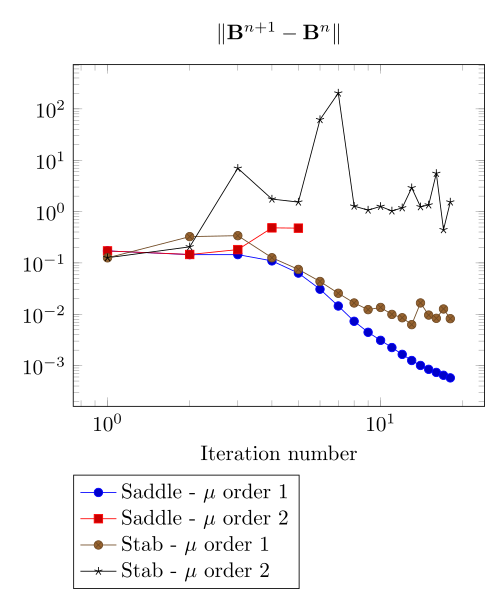
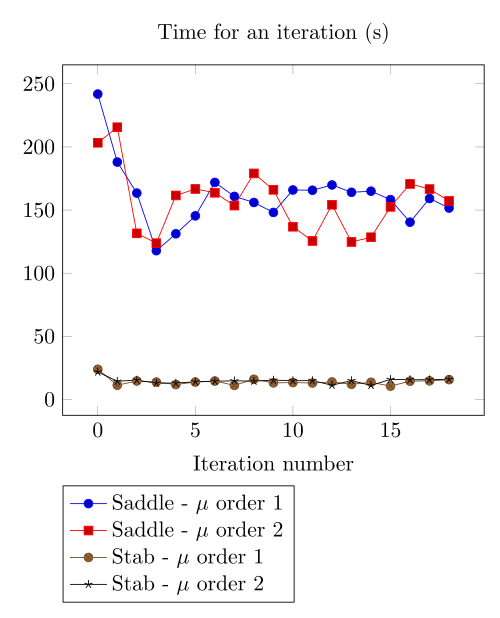
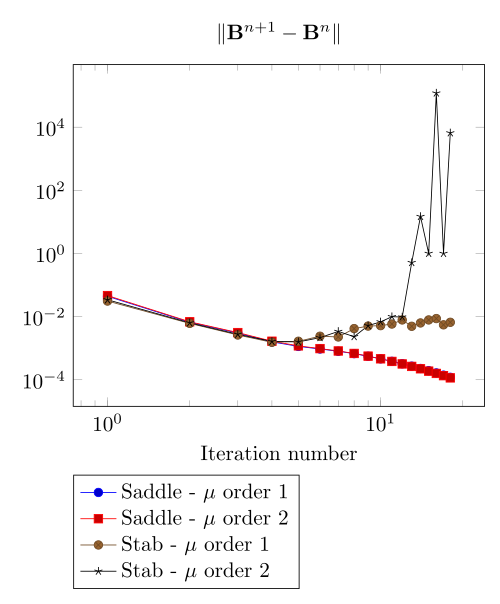
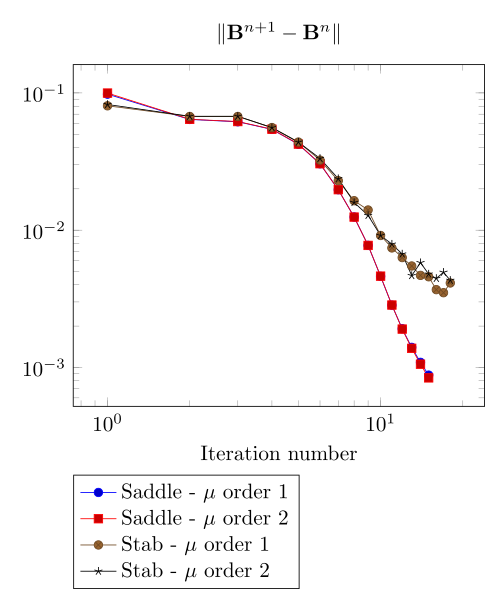
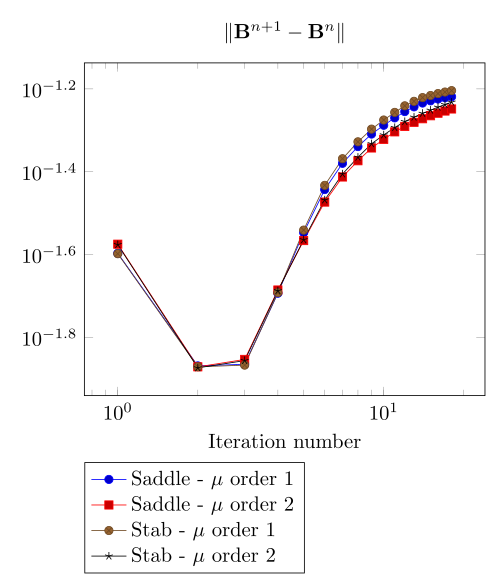
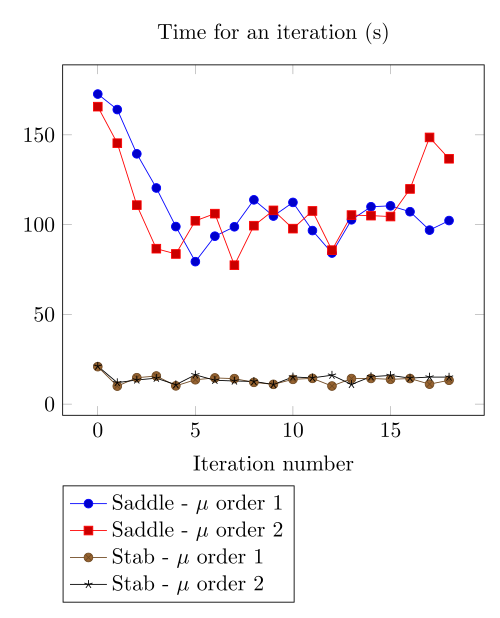
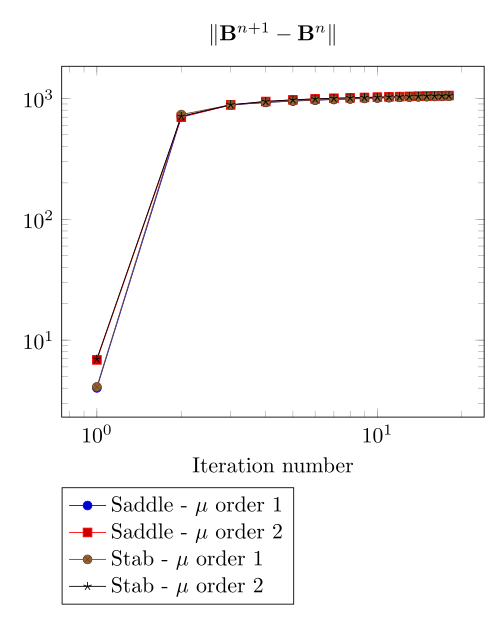
We begin with the smoothiest \(B-H\) relation. At very low current density, both formulations (saddle, regularized), both algorithms (Picard, Polarization) with the two kinds of \(\mu\) discretizaion converge.

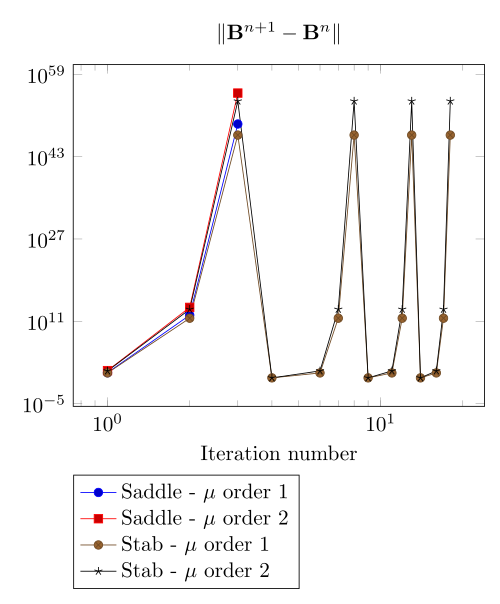
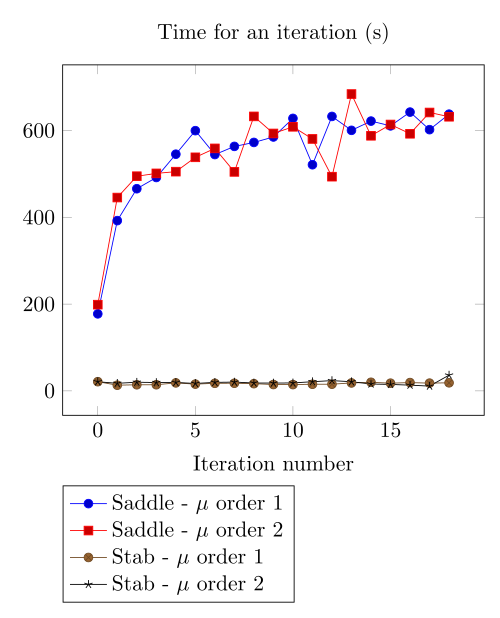
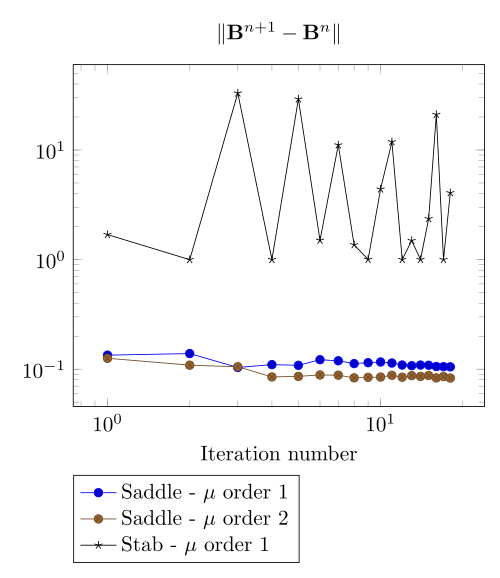
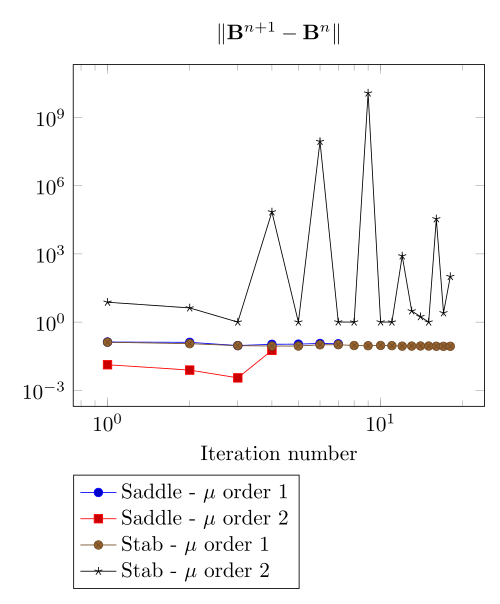
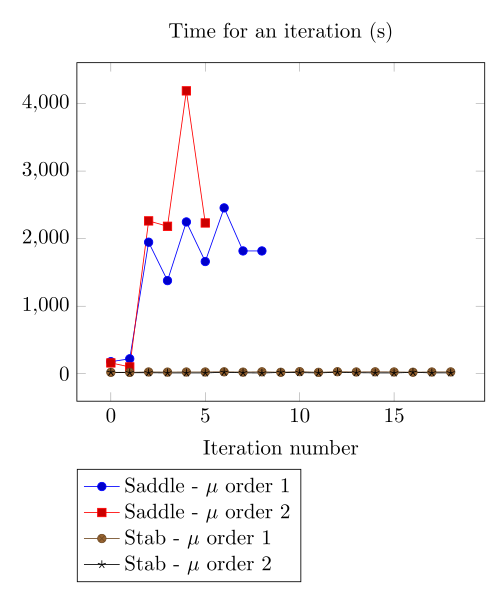
Here we show that the polarization method is not robust against high density current.

4.1.1. Mesh 1

500 AT - Picard mesh 1 AT 500 algo 0 mod inductor3d feel

500 AT - Picard mesh 1 AT 500 algo 0 mod inductor3d feel time

500 AT - Polarization mesh 1 AT 500 algo 1 mod inductor3d feel

500 AT - Polarization mesh 1 AT 500 algo 1 mod inductor3d feel time

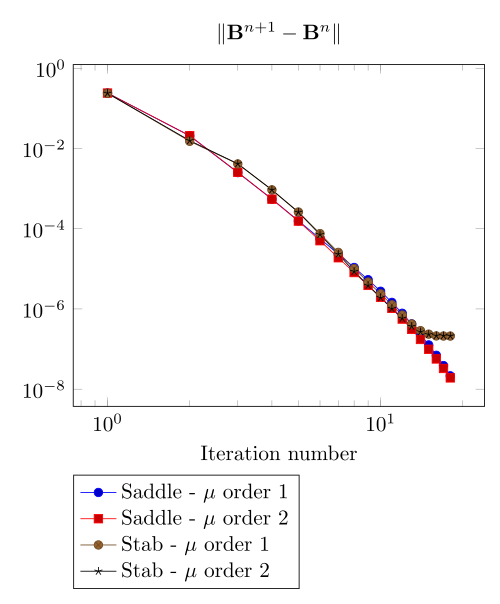
1000 AT - Picard mesh 1 AT 1000 algo 0 mod inductor3d feel

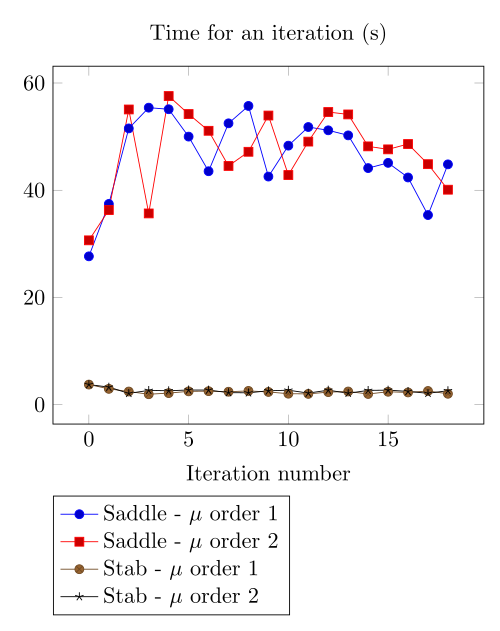
1000 AT - Picard mesh 1 AT 1000 algo 0 mod inductor3d feel time

1000 AT - Polarization mesh 1 AT 1000 algo 1 mod inductor3d feel

1000 AT - Polarization mesh 1 AT 1000 algo 1 mod inductor3d feel time

2000 AT - Picard mesh 1 AT 2000 algo 0 mod inductor3d feel

2000 AT - Picard mesh 1 AT 2000 algo 0 mod inductor3d feel time

2000 AT - Polarization mesh 1 AT 2000 algo 1 mod inductor3d feel

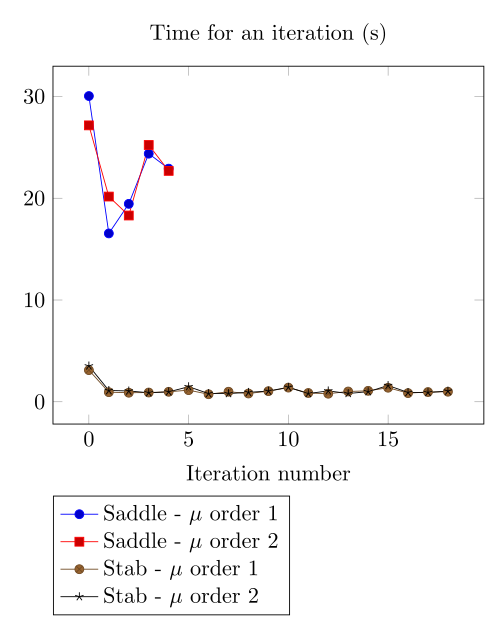
2000 AT - Polarization mesh 1 AT 2000 algo 1 mod inductor3d feel time

3000 AT - Picard mesh 1 AT 3000 algo 0 mod inductor3d feel

3000 AT - Picard mesh 1 AT 3000 algo 0 mod inductor3d feel time

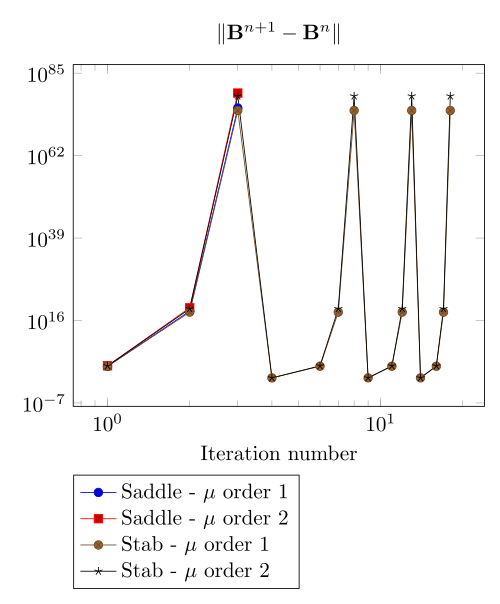
3000 AT - Polarization mesh 1 AT 3000 algo 1 mod inductor3d feel

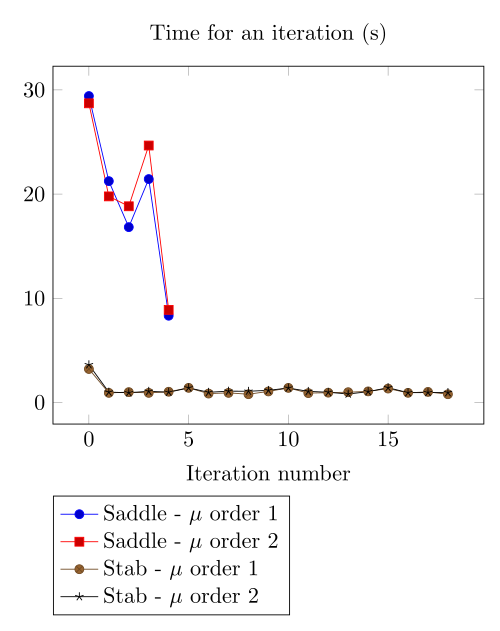
3000 AT - Polarization mesh 1 AT 3000 algo 1 mod inductor3d feel time

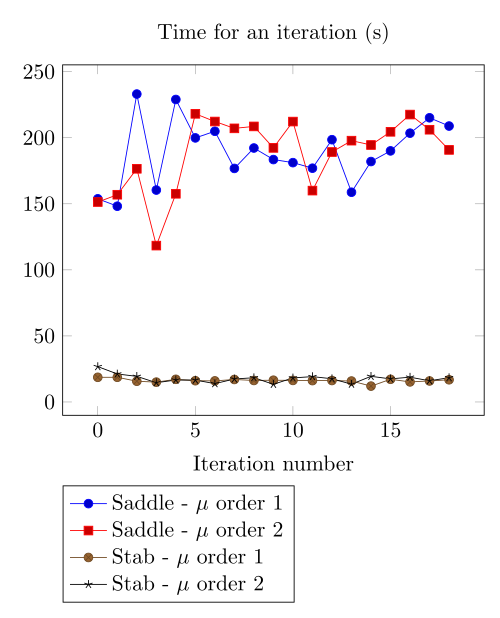
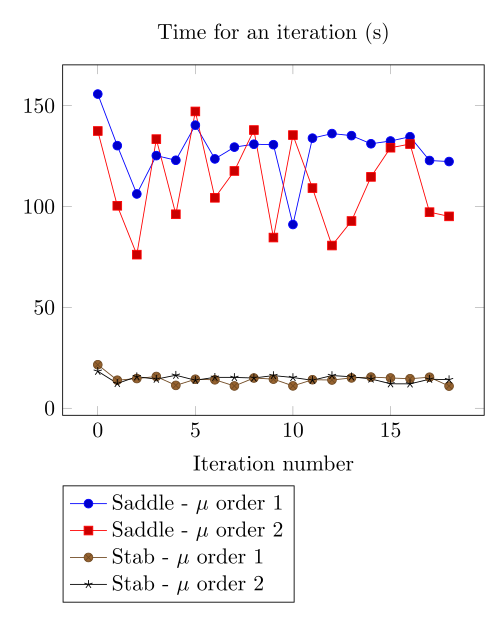
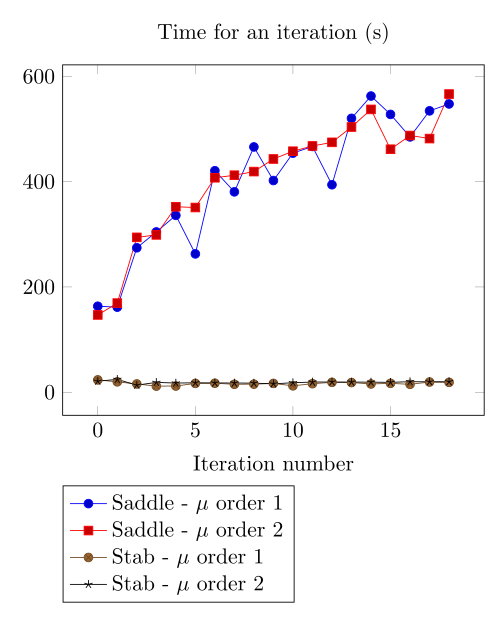
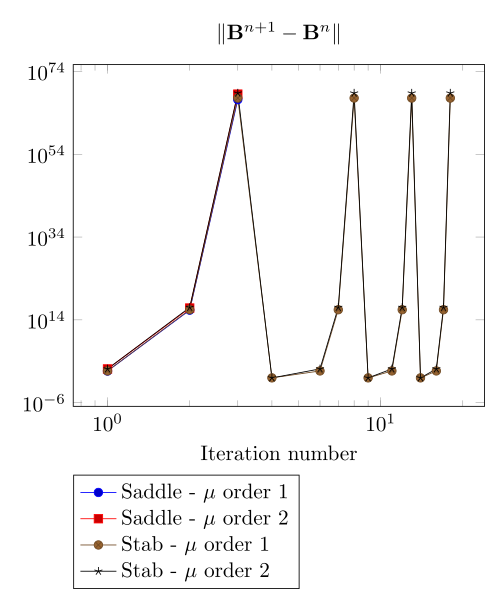
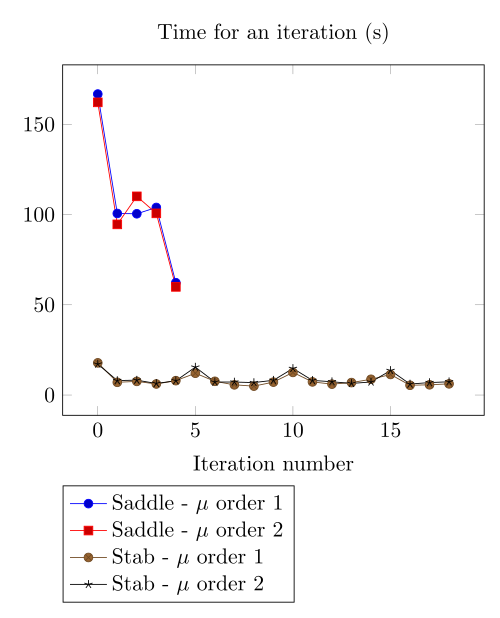
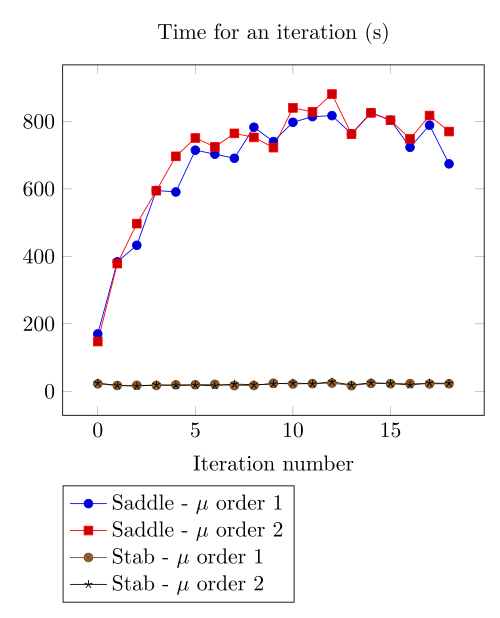
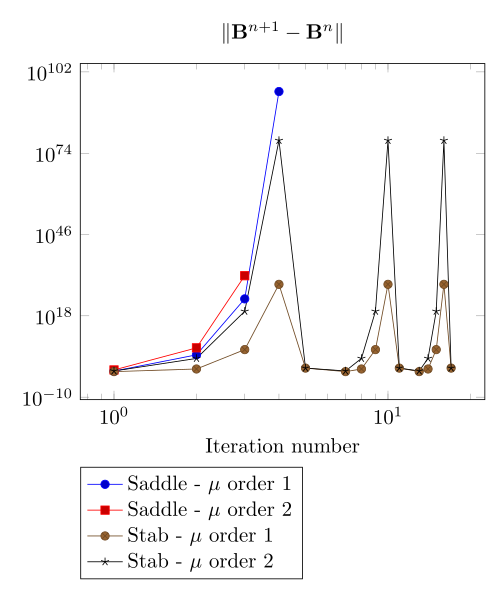
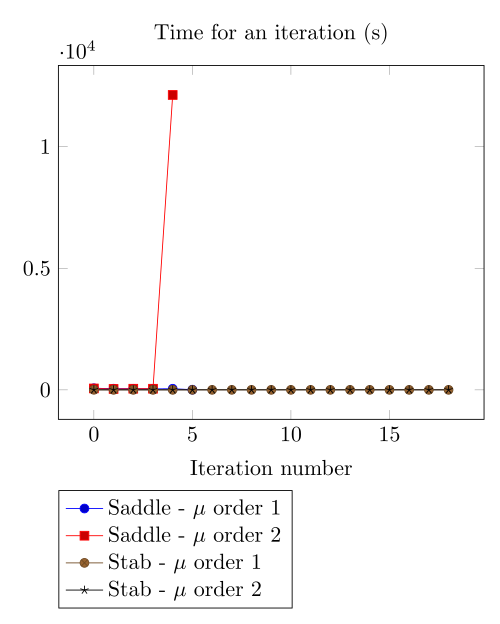
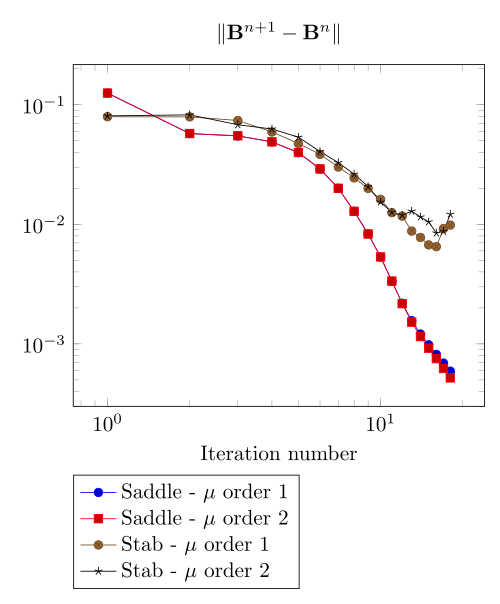
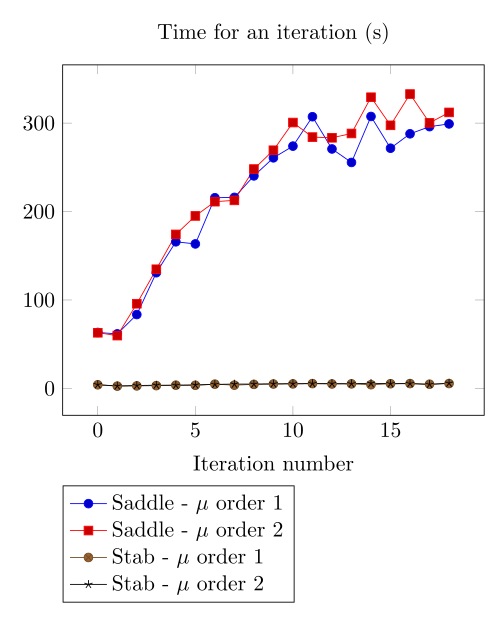
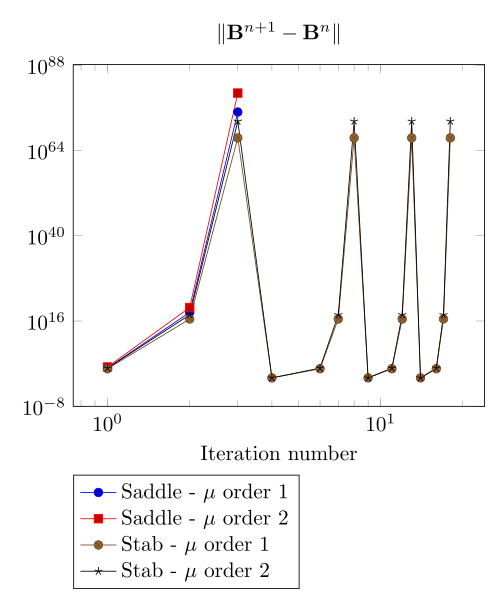
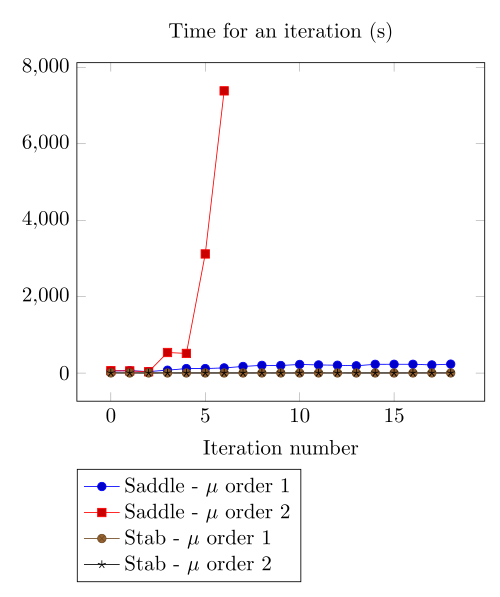
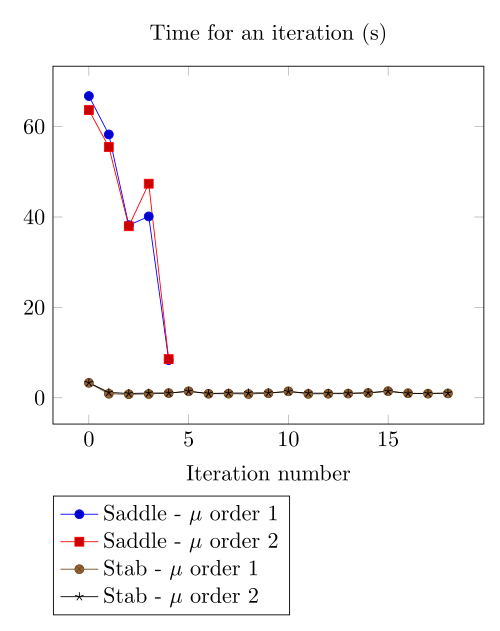
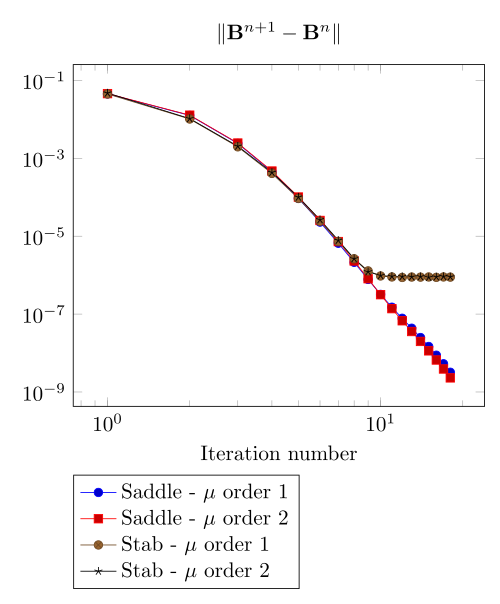
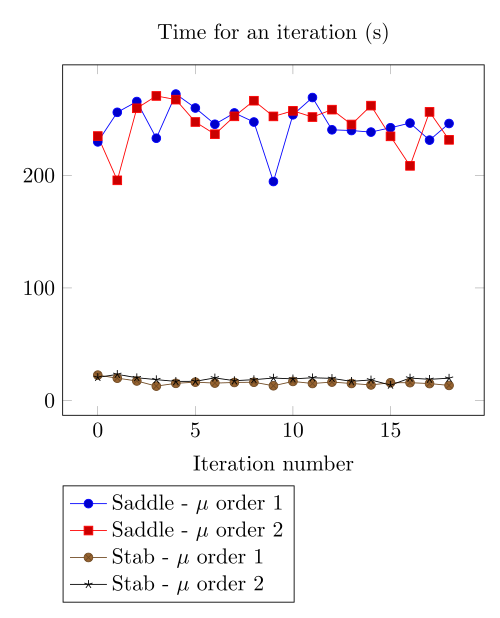
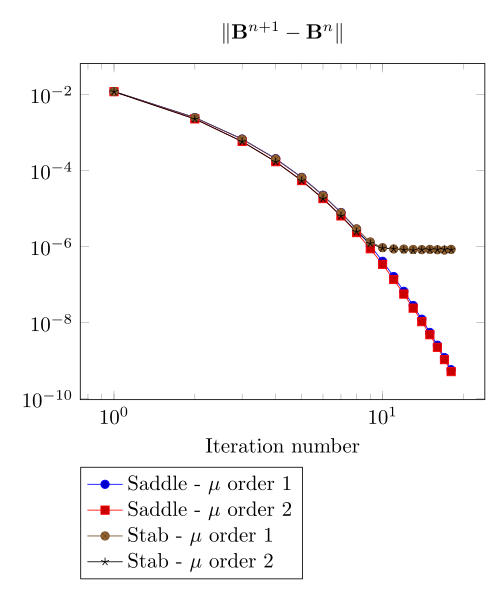
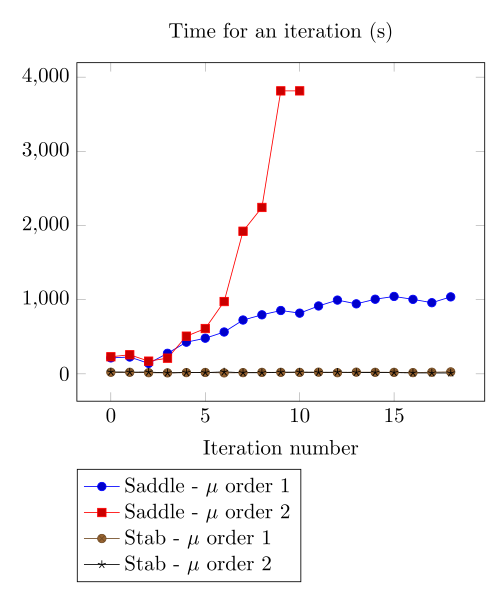
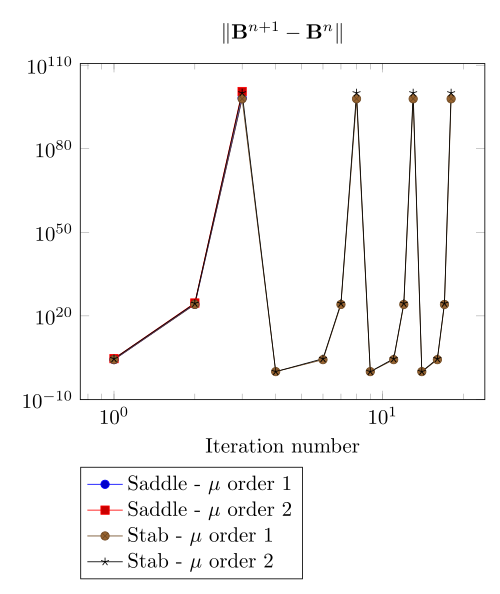
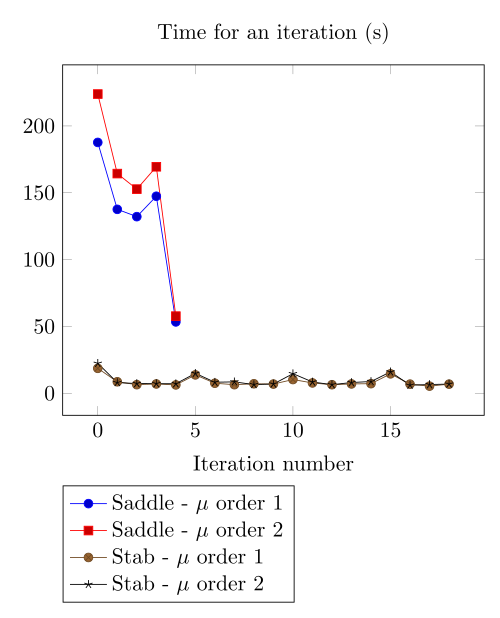
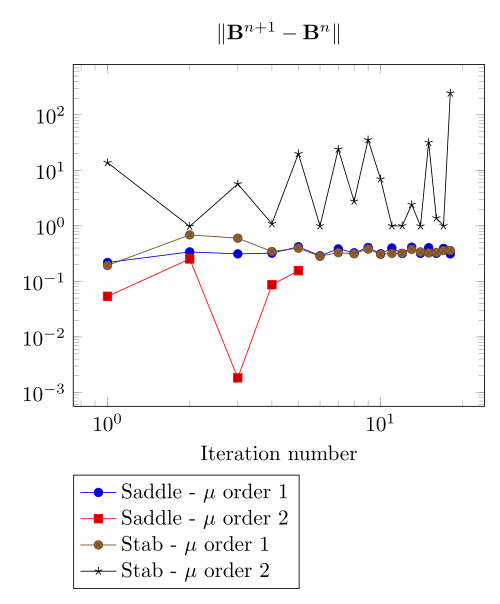
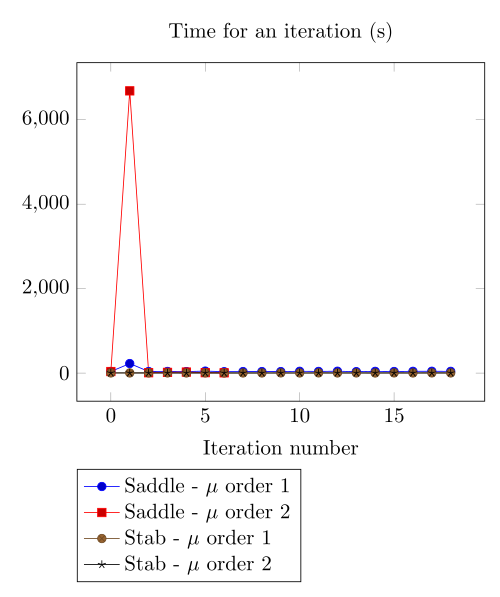
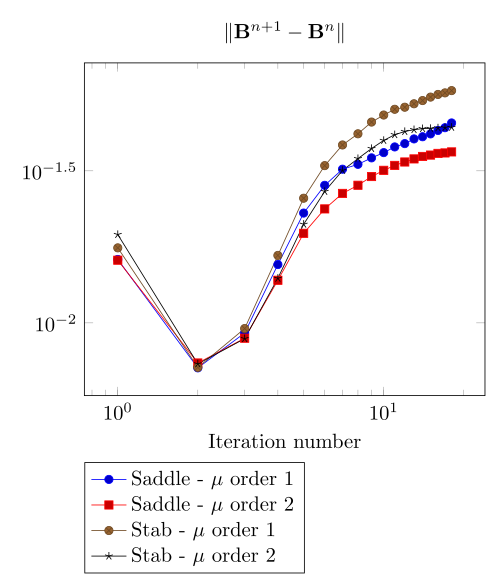
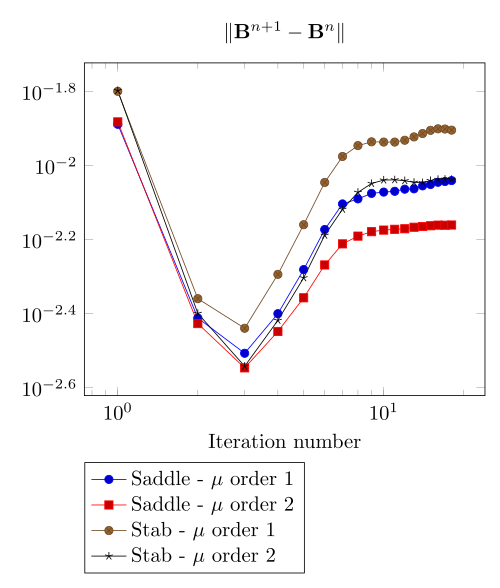
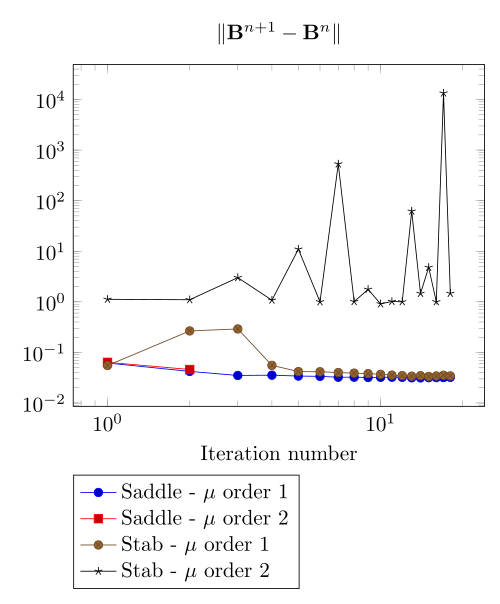
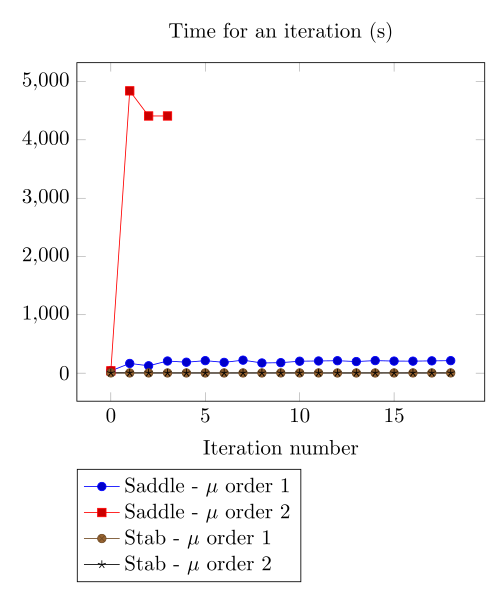
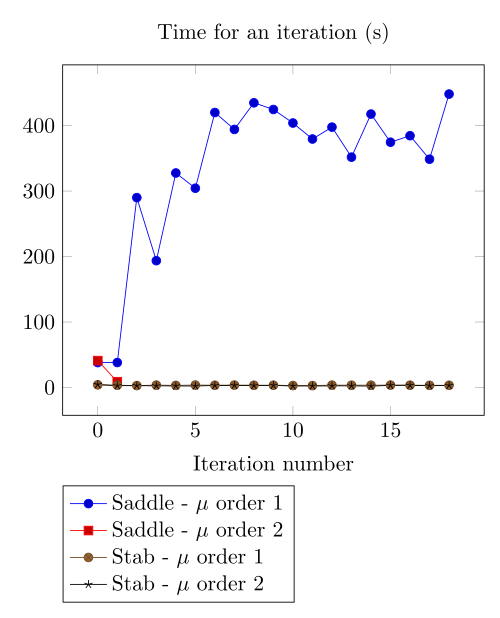
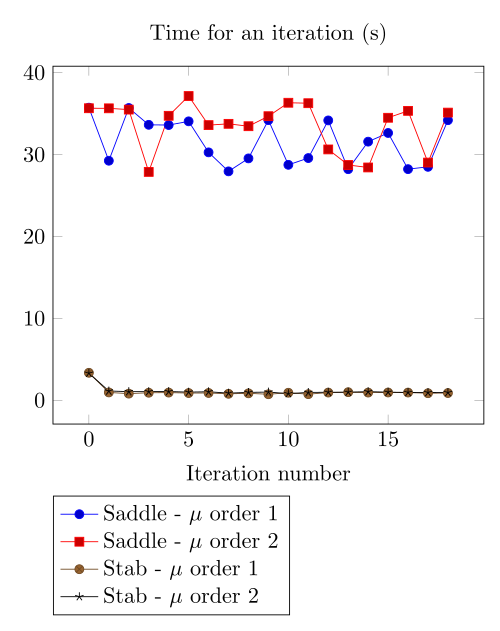
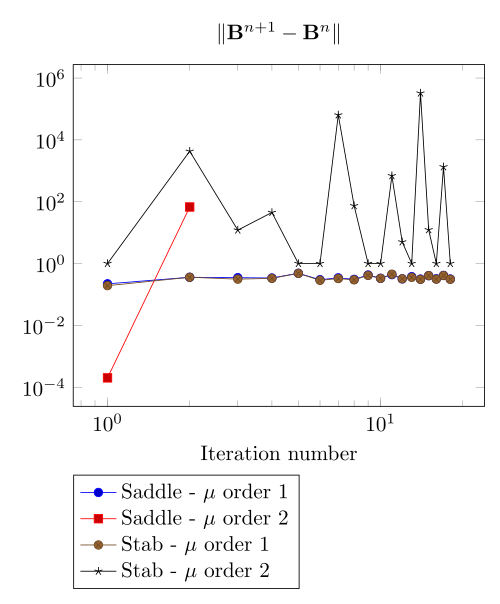
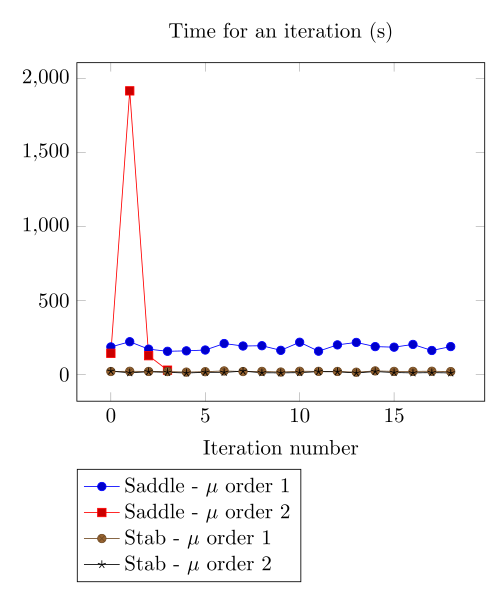
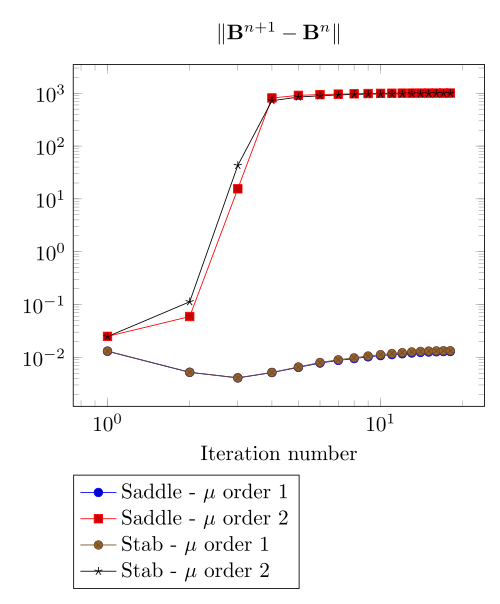
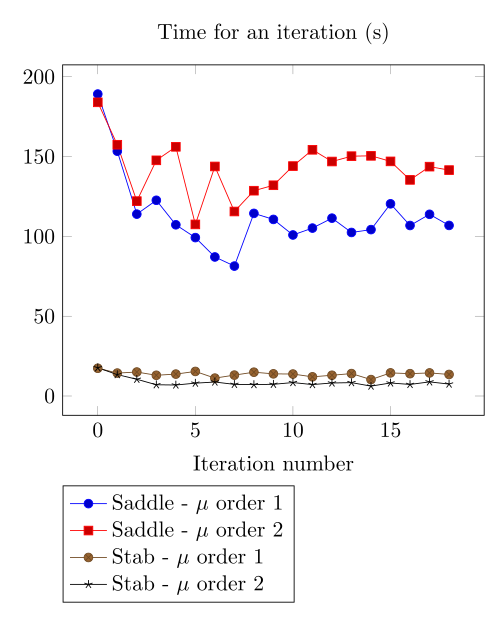
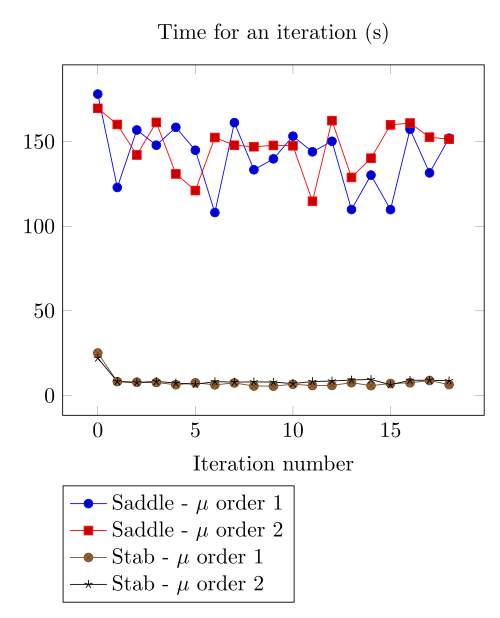
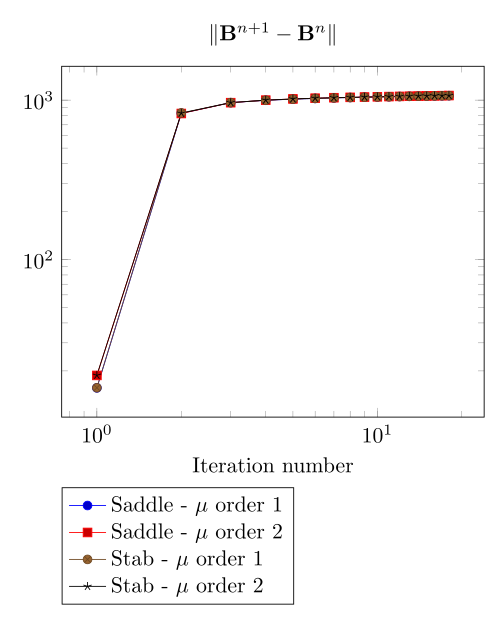
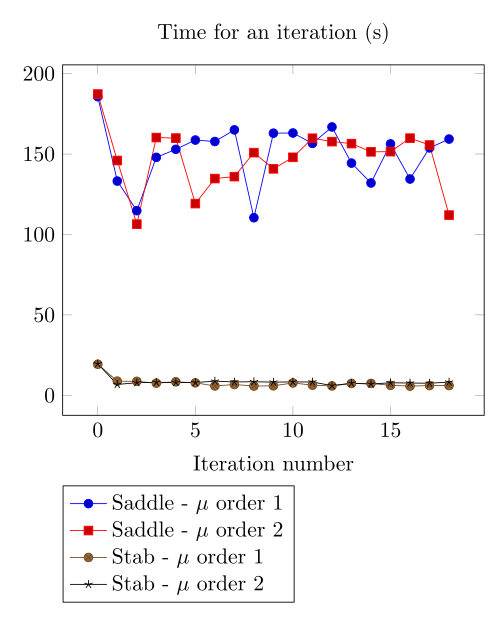
At first, we can observe - the Polarization method does not handle the hight current density, - the regularized formulation is always faster, - the saddle point formulation is always more accurate, - the \(\mu\) space discretization has a little impact in the convergence.

4.1.2. Mesh 2

500 AT - Picard mesh 2 AT 500 algo 0 mod inductor3d feel

500 AT - Picard mesh 2 AT 500 algo 0 mod inductor3d feel time

500 AT - Polarization mesh 2 AT 500 algo 1 mod inductor3d feel

500 AT - Polarization mesh 2 AT 500 algo 1 mod inductor3d feel time

1000 AT - Picard mesh 2 AT 1000 algo 0 mod inductor3d feel

1000 AT - Picard mesh 2 AT 1000 algo 0 mod inductor3d feel time

1000 AT - Polarization mesh 2 AT 1000 algo 1 mod inductor3d feel

1000 AT - Polarization mesh 2 AT 1000 algo 1 mod inductor3d feel time

2000 AT - Picard mesh 2 AT 2000 algo 0 mod inductor3d feel

2000 AT - Picard mesh 2 AT 2000 algo 0 mod inductor3d feel time

2000 AT - Polarization mesh 2 AT 2000 algo 1 mod inductor3d feel

2000 AT - Polarization mesh 2 AT 2000 algo 1 mod inductor3d feel time

3000 AT - Picard mesh 2 AT 3000 algo 0 mod inductor3d feel

3000 AT - Picard mesh 2 AT 3000 algo 0 mod inductor3d feel time

3000 AT - Polarization mesh 2 AT 3000 algo 1 mod inductor3d feel

3000 AT - Polarization mesh 2 AT 3000 algo 1 mod inductor3d feel time

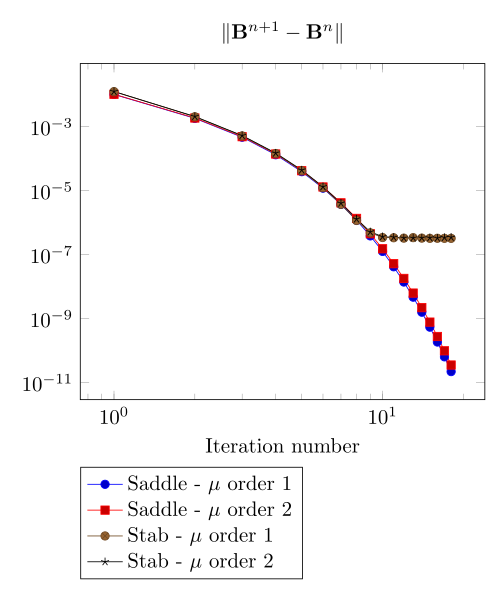
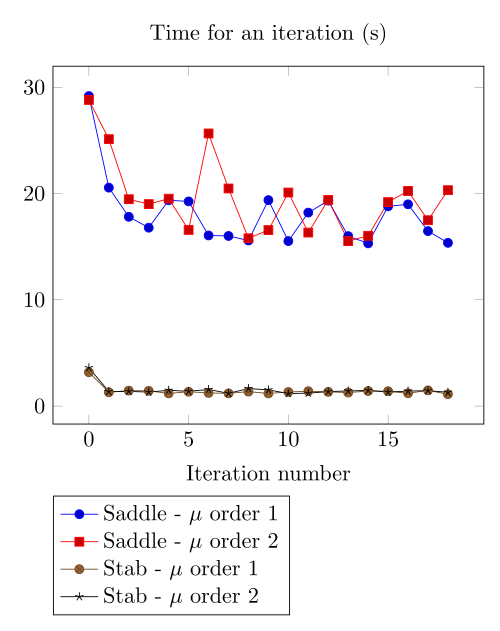
Increasing the dof density does not improve here the convergence of failling method.

4.2. Intermediate non linear curve

4.2.1. Mesh 1

500 AT - Picard mesh 1 AT 500 algo 0 mod sigma phi

500 AT - Picard mesh 1 AT 500 algo 0 mod sigma phi time

500 AT - Polarization mesh 1 AT 500 algo 1 mod sigma phi

500 AT - Polarization mesh 1 AT 500 algo 1 mod sigma phi time

1000 AT - Picard mesh 1 AT 1000 algo 0 mod sigma phi

1000 AT - Picard mesh 1 AT 1000 algo 0 mod sigma phi time

1000 AT - Polarization mesh 1 AT 1000 algo 1 mod sigma phi

1000 AT - Polarization mesh 1 AT 1000 algo 1 mod sigma phi time

2000 AT - Picard mesh 1 AT 2000 algo 0 mod sigma phi

2000 AT - Picard mesh 1 AT 2000 algo 0 mod sigma phi time

2000 AT - Polarization mesh 1 AT 2000 algo 1 mod sigma phi

2000 AT - Polarization mesh 1 AT 2000 algo 1 mod sigma phi time

3000 AT - Picard mesh 1 AT 3000 algo 0 mod sigma phi

3000 AT - Picard mesh 1 AT 3000 algo 0 mod sigma phi time

3000 AT - Polarization mesh 1 AT 3000 algo 1 mod sigma phi

3000 AT - Polarization mesh 1 AT 3000 algo 1 mod sigma phi time

4.2.2. Mesh 2

500 AT - Picard mesh 2 AT 500 algo 0 mod sigma phi

500 AT - Picard mesh 2 AT 500 algo 0 mod sigma phi time

500 AT - Polarization mesh 2 AT 500 algo 1 mod sigma phi

500 AT - Polarization mesh 2 AT 500 algo 1 mod sigma phi time

1000 AT - Picard mesh 2 AT 1000 algo 0 mod sigma phi

1000 AT - Picard mesh 2 AT 1000 algo 0 mod sigma phi time

1000 AT - Polarization mesh 2 AT 1000 algo 1 mod sigma phi

1000 AT - Polarization mesh 2 AT 1000 algo 1 mod sigma phi time

2000 AT - Picard mesh 2 AT 2000 algo 0 mod sigma phi

2000 AT - Picard mesh 2 AT 2000 algo 0 mod sigma phi time

2000 AT - Polarization mesh 2 AT 2000 algo 1 mod sigma phi

2000 AT - Polarization mesh 2 AT 2000 algo 1 mod sigma phi time

3000 AT - Picard mesh 2 AT 3000 algo 0 mod sigma phi

3000 AT - Picard mesh 2 AT 3000 algo 0 mod sigma phi time

3000 AT - Polarization mesh 2 AT 3000 algo 1 mod sigma phi

3000 AT - Polarization mesh 2 AT 3000 algo 1 mod sigma phi time

4.3. TEAM Workshop 13 non linear curve

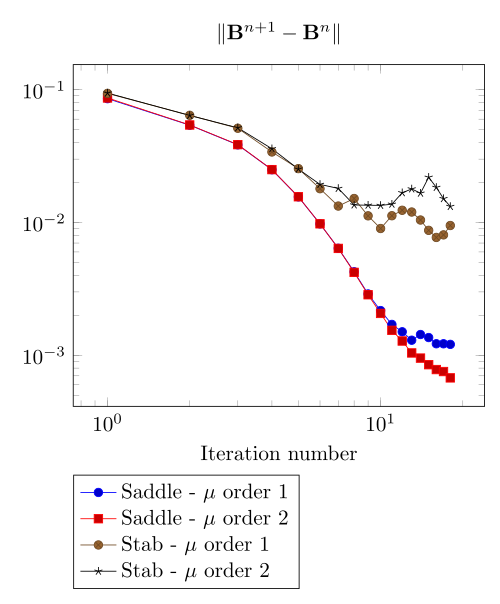
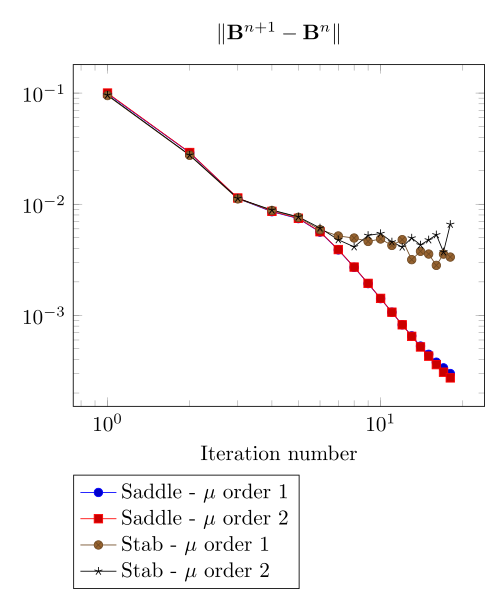
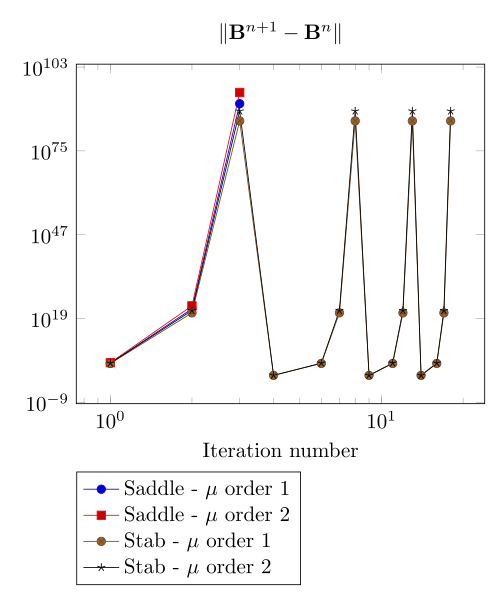
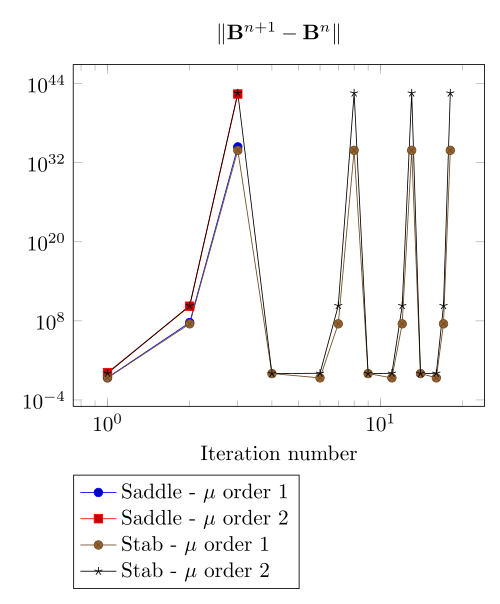
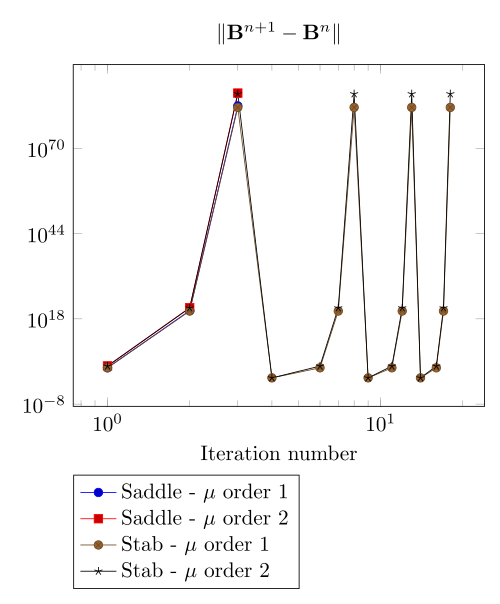
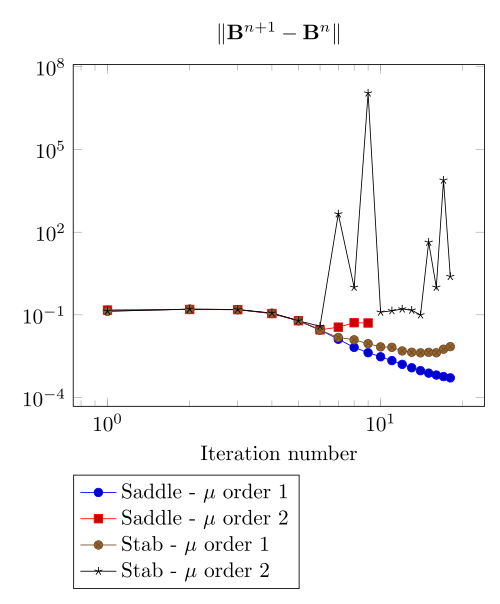
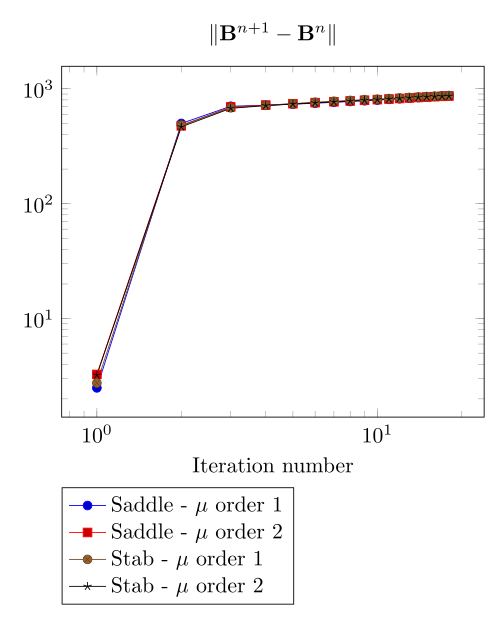
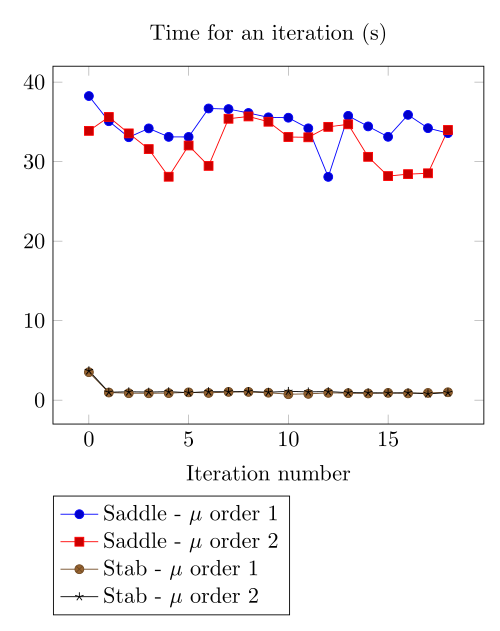
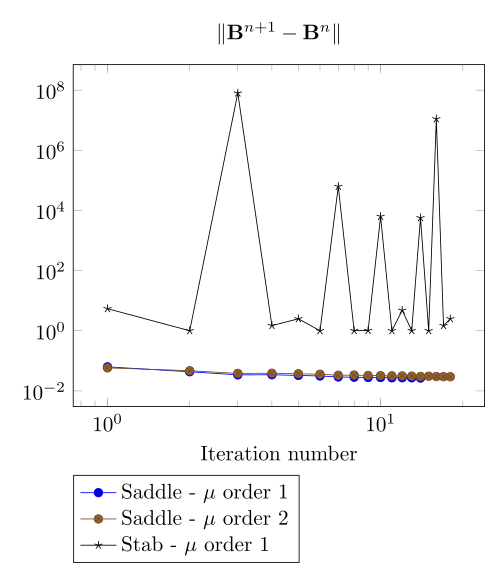
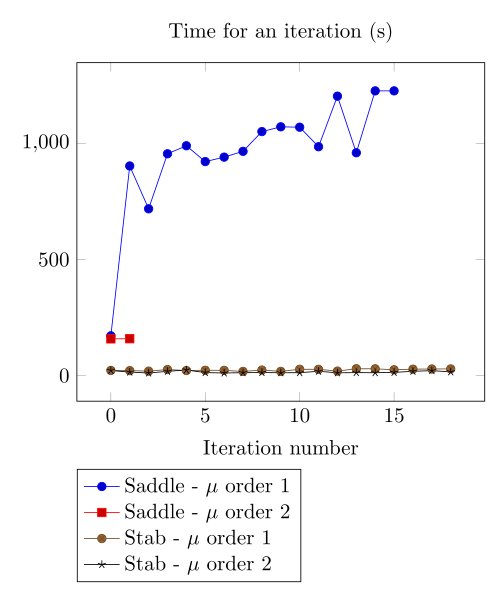
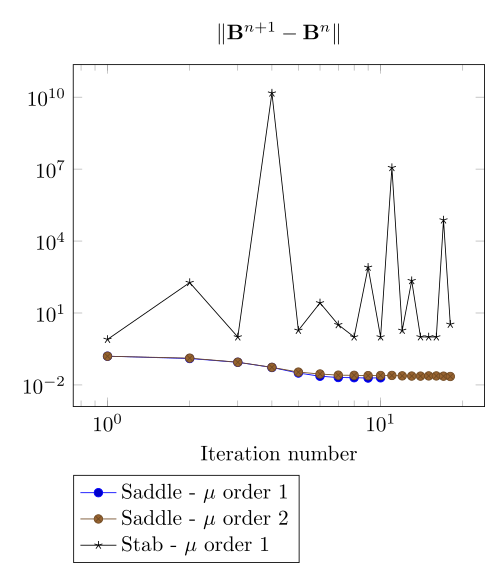
We have observed with the getDP relation the polarization method is not robust. We have observed with the \(\Sigma-\Phi\) relation the regularity of the relation can be a bottleneck.

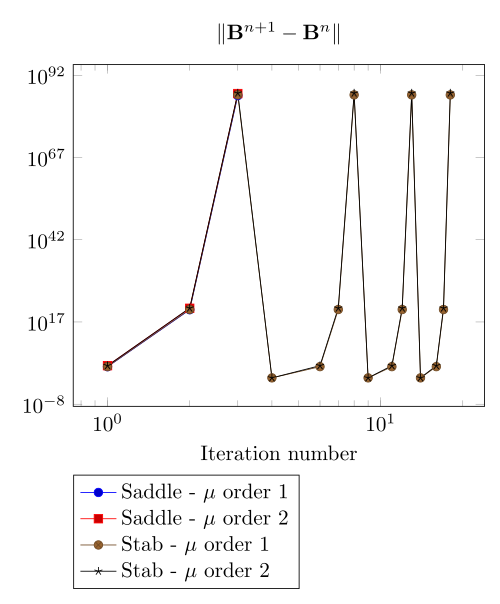
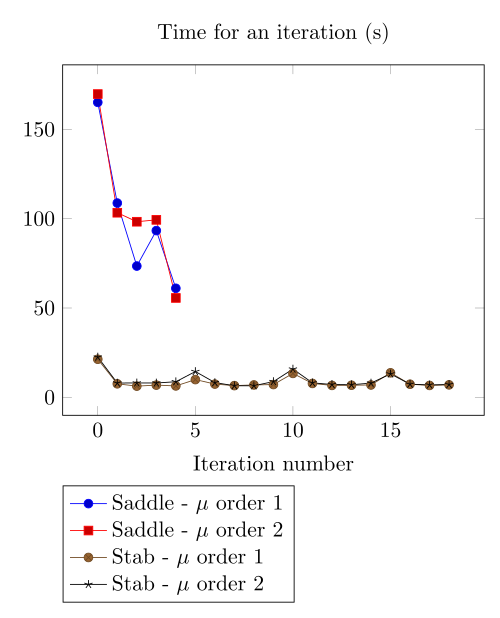
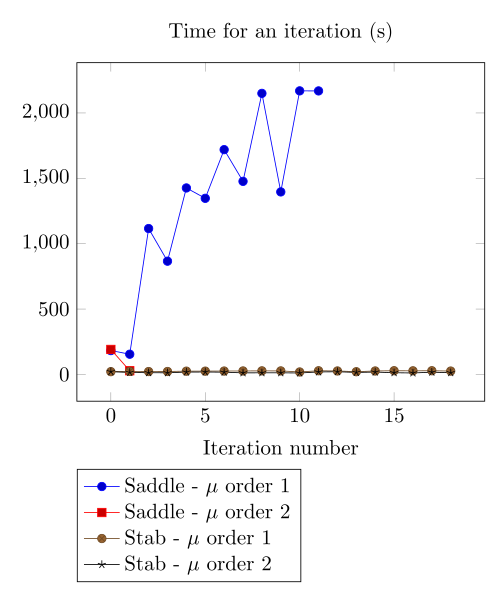
Here, we show the team Workshop 13 \(B-H\) relation provide us - at best - non fully convergent simulations and only saddle-point formulation with picard algorithm can be run.

4.3.1. Mesh 1

500 AT - Picard mesh 1 AT 500 algo 0 mod tws

500 AT - Picard mesh 1 AT 500 algo 0 mod tws time

500 AT - Polarization mesh 1 AT 500 algo 1 mod tws

500 AT - Polarization mesh 1 AT 500 algo 1 mod tws time

1000 AT - Picard mesh 1 AT 1000 algo 0 mod tws

1000 AT - Picard mesh 1 AT 1000 algo 0 mod tws time

1000 AT - Polarization mesh 1 AT 1000 algo 1 mod tws

1000 AT - Polarization mesh 1 AT 1000 algo 1 mod tws time

2000 AT - Picard mesh 1 AT 2000 algo 0 mod tws

2000 AT - Picard mesh 1 AT 2000 algo 0 mod tws time

2000 AT - Polarization mesh 1 AT 2000 algo 1 mod tws

2000 AT - Polarization mesh 1 AT 2000 algo 1 mod tws time

3000 AT - Picard mesh 1 AT 3000 algo 0 mod tws

3000 AT - Picard mesh 1 AT 3000 algo 0 mod tws time

3000 AT - Polarization mesh 1 AT 3000 algo 1 mod tws

3000 AT - Polarization mesh 1 AT 3000 algo 1 mod tws time

4.3.2. Mesh 2

500 AT - Picard mesh 2 AT 500 algo 0 mod tws

500 AT - Picard mesh 2 AT 500 algo 0 mod tws time

500 AT - Polarization mesh 2 AT 500 algo 1 mod tws

500 AT - Polarization mesh 2 AT 500 algo 1 mod tws time

1000 AT - Picard mesh 2 AT 1000 algo 0 mod tws

1000 AT - Picard mesh 2 AT 1000 algo 0 mod tws time

1000 AT - Polarization mesh 2 AT 1000 algo 1 mod tws

1000 AT - Polarization mesh 2 AT 1000 algo 1 mod tws time

2000 AT - Picard mesh 2 AT 2000 algo 0 mod tws

2000 AT - Picard mesh 2 AT 2000 algo 0 mod tws time

2000 AT - Polarization mesh 2 AT 2000 algo 1 mod tws

2000 AT - Polarization mesh 2 AT 2000 algo 1 mod tws time

3000 AT - Picard mesh 2 AT 3000 algo 0 mod tws

3000 AT - Picard mesh 2 AT 3000 algo 0 mod tws time

3000 AT - Polarization mesh 2 AT 3000 algo 1 mod tws

3000 AT - Polarization mesh 2 AT 3000 algo 1 mod tws time

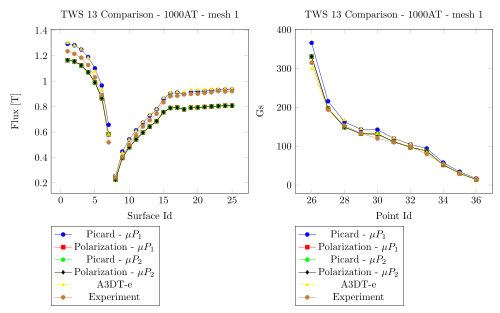
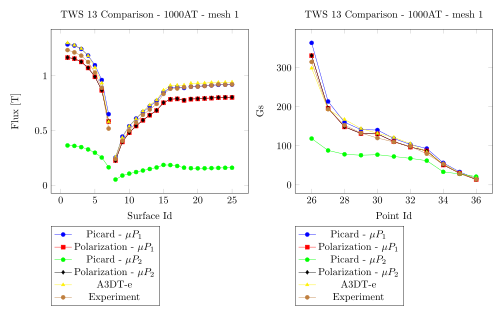
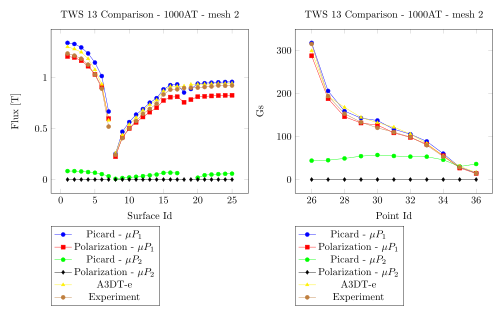
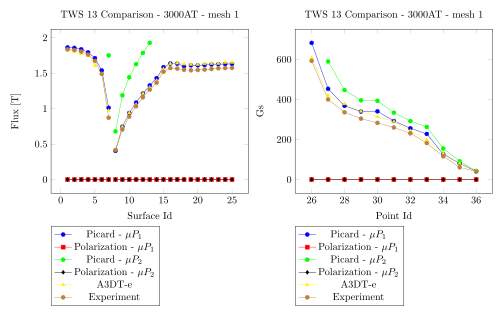
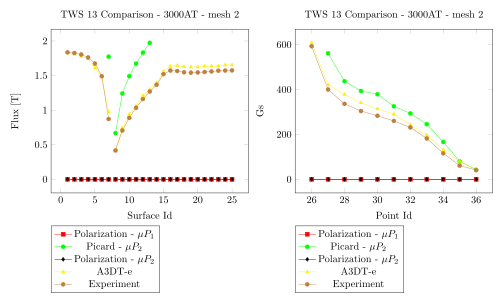
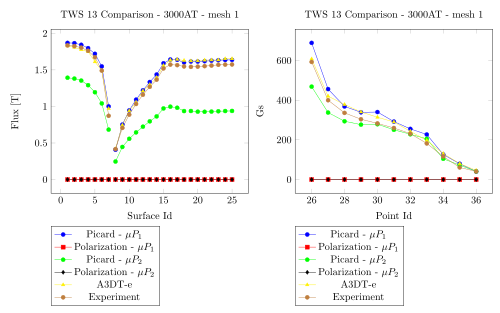
5. Comparision with Team Workshop 13

1000 AT - Mesh 1 - Saddle tws13 saddle 1 1000

1000 AT - Mesh 2 - Saddle tws13 saddle 2 1000

1000 AT - Mesh 1 - Regularized tws13 stab 1 1000

1000 AT - Mesh 2 - Regularized tws13 stab 2 1000

3000 AT - Mesh 1 - Saddle tws13 saddle 1 3000

3000 AT - Mesh 2 - Saddle tws13 saddle 2 3000

3000 AT - Mesh 1 - Regularized tws13 stab 1 3000

3000 AT - Mesh 2 - Regularized tws13 stab 2 3000

6. Remarks

Polarization or Picard ?

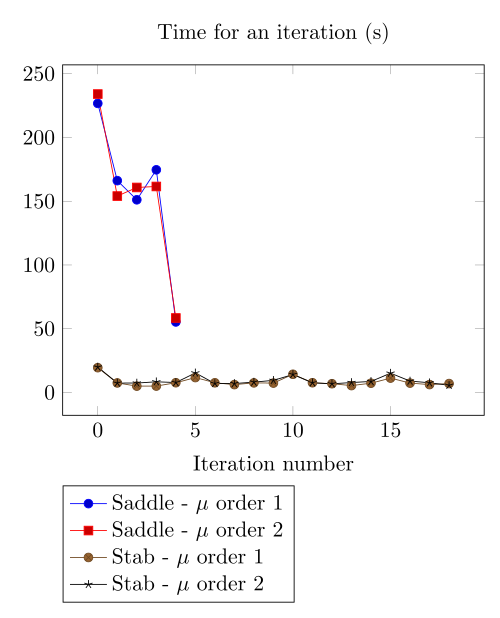
At first, we can be dispointed with the very small advantage the Polarization method provide considering the computing time. It has to be higlighted the update() method - for the non linear right hand side or the magnetic permeability - has an effect on the magnetic concrete. As long as the ratio of magnetic concrete volume in the whole volume of computation is always little, we are not surprised to face a very little improvement in the method. Actually, rebuilding the preconditioner does seem to be that time consuming.

Saddle or Regularizd ?

Considering our results, we recommend the following strategy: - run the regularized formulation until a stationnary point is found, - use the current \(\mathbb{A}\) as an initial guess for the saddle point method.

\(\mu\) discretization

Our calculus has not shown a sufficient difference to definitely chose.

7. Propositions

Here the ideas we do not have time to test.

7.1. Polarization

The polarization generate a right hand side that can present huge variations - see the \(B-H\) curve for \(B \approx 1.8\) for example. In the present geometry, the maximum of \(B\) is achieved at the boundary of the ferromagnetic concrete. That is the non linear right hand side is discontinuous along the boundary of the ferromagnetic concrete, with a huge variation. We recommend to test the \(L_2\) projection of the non linear right hand side in the whole domain to smooth it, with a smoothing parameter decreasing with the iterations to decrease the effect of this projection.

7.2. Continuity

Considering the convergence is mainly linked to the current density, a contiuation algorithm has to be testesd.

7.3. Mixing Polarization and Picard.

The Polarization method reads:

\[B = \mu_{opt} H + I\]

where the picard method reads:

\[B = \mu_0 \mu_r H\]

The idea we propose is to write:

\[\begin{aligned} B^{(n)} &= \mu_{opt} H ^{(n)} + I^{(n)} \\ &= \mu_0 \mu_r^{(n)} H^{(n)} \end{aligned}\]

That is

\[\mu_r^{(n)} = \frac{\mu_{opt}}{\mu_0} + \frac{1}{\mu_0 H^{(n)}} I^{(n)}\]

That is we can transfert the non linearity from the right hand side to the matrix whenever we have to.