NAFEMS LE1 Benchmarck

This benchmark is extract from the Abaqus Benchmarks Manual.

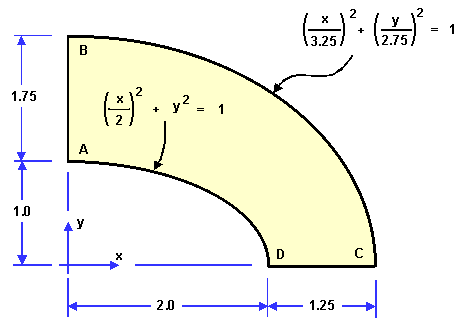
1. Definition

We focus on the LE1 benchmarks in particular.

2. Running the case

The command line to run this case is

mpirun -np 4 feelpp_toolbox_solid --case "github:{path:toolboxes/solid/cases/NAFEMS-LE1}"

Case option

--case "github:{path:toolboxes/solid/cases/NAFEMS-LE1}"

3. Data files

The case data files are available in Github here

CFG file - [Edit the file]
JSON file - [Edit the file]

3.1. Geometry

The geometry is given here by :

Figure 1. 2D Geometry

3.2. Boundary conditions

We set:

\(u_y = 0\) on DC
\(u_x = 0\) on AB
\(\bar{\bar{\varepsilon}}\cdot\mathbf{n}=1e^7\) on BC.

4. Inputs

We have the following parameters:

Table 1. Inputs
Name	Value
\(E\)	\(210\, GPa\)
\(\nu\)	\(0.3\)
\(\rho\)	\(7800\, kg/m^2\)

5. Outputs

We compare the value of \(\sigma_{yy}\) at the point D. The reference value is \(92.7\, MPa\).

6. Results

Here are the verifications of the benchmarks: .Checkers Output

+---------------------------------------------------------------------------------------------------------+
| Checkers : solid                                                                                        |
+---------------------------------------------------------------------------------------------------------+
| +-----------+-----------------------------+--------------+--------------+--------------+--------------+ |
| | check     | name                        | measure      | reference    | error        | tolerance    | |
| +===========+=============================+==============+==============+==============+==============+ |
| | [success] | Points_pointD_expr_sigma_yy | 9.268058e+07 | 9.270000e+07 | 2.095100e-04 | 1.000000e-02 | |
| +-----------+-----------------------------+--------------+--------------+--------------+--------------+ |
+---------------------------------------------------------------------------------------------------------+

The value of \(\sigma_{yy}\) at the point D is \(94.09\, MPa\) for \(32 000\) dofs, which is \(1.49%\) higher than the target.

One possibility to get a more accurate output is to use a mixed formulation, where the stress tensor would also be an unknown.

We now display the displacement field and the Vonmises stress field.

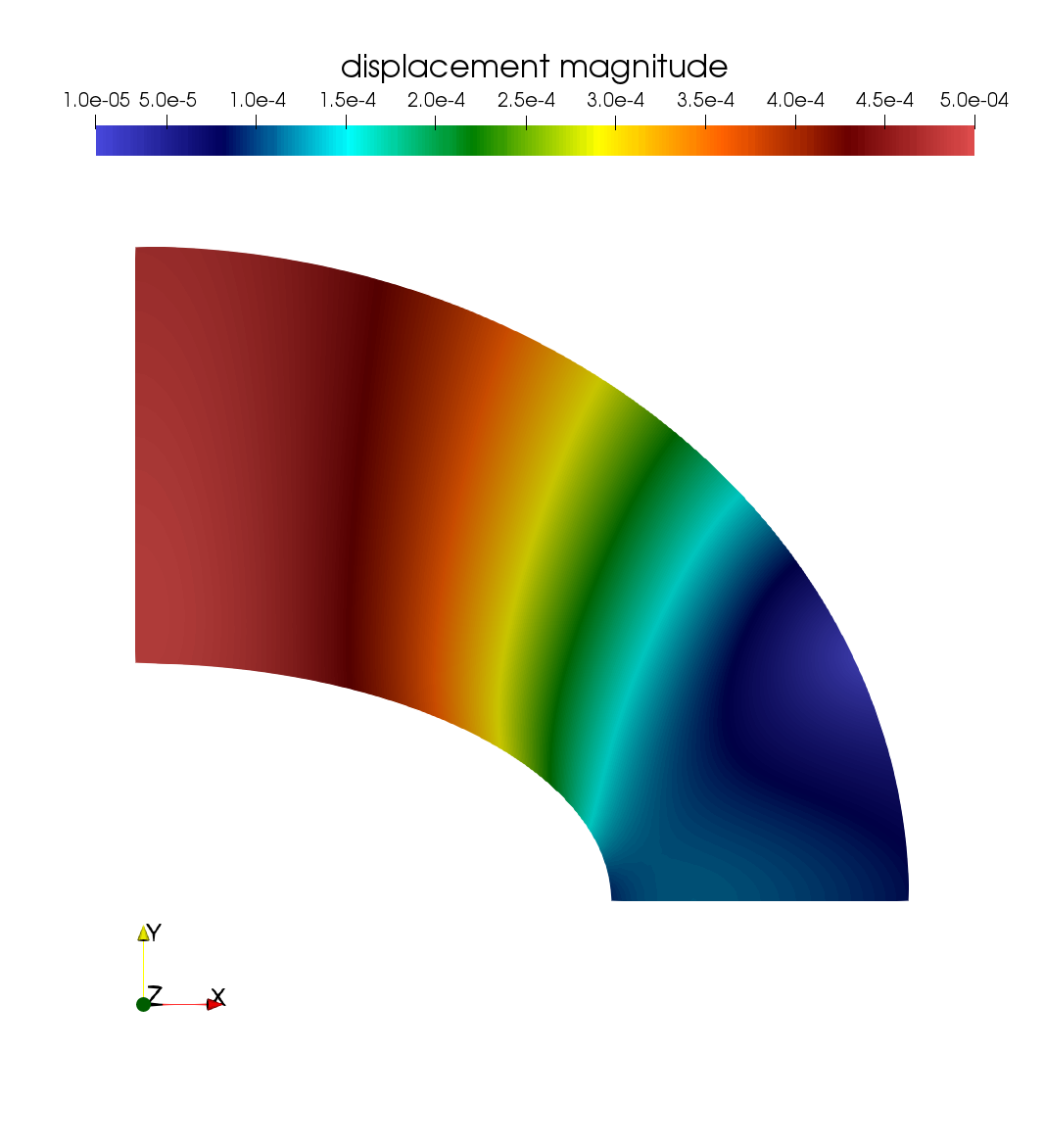
Figure 2. Displacement field

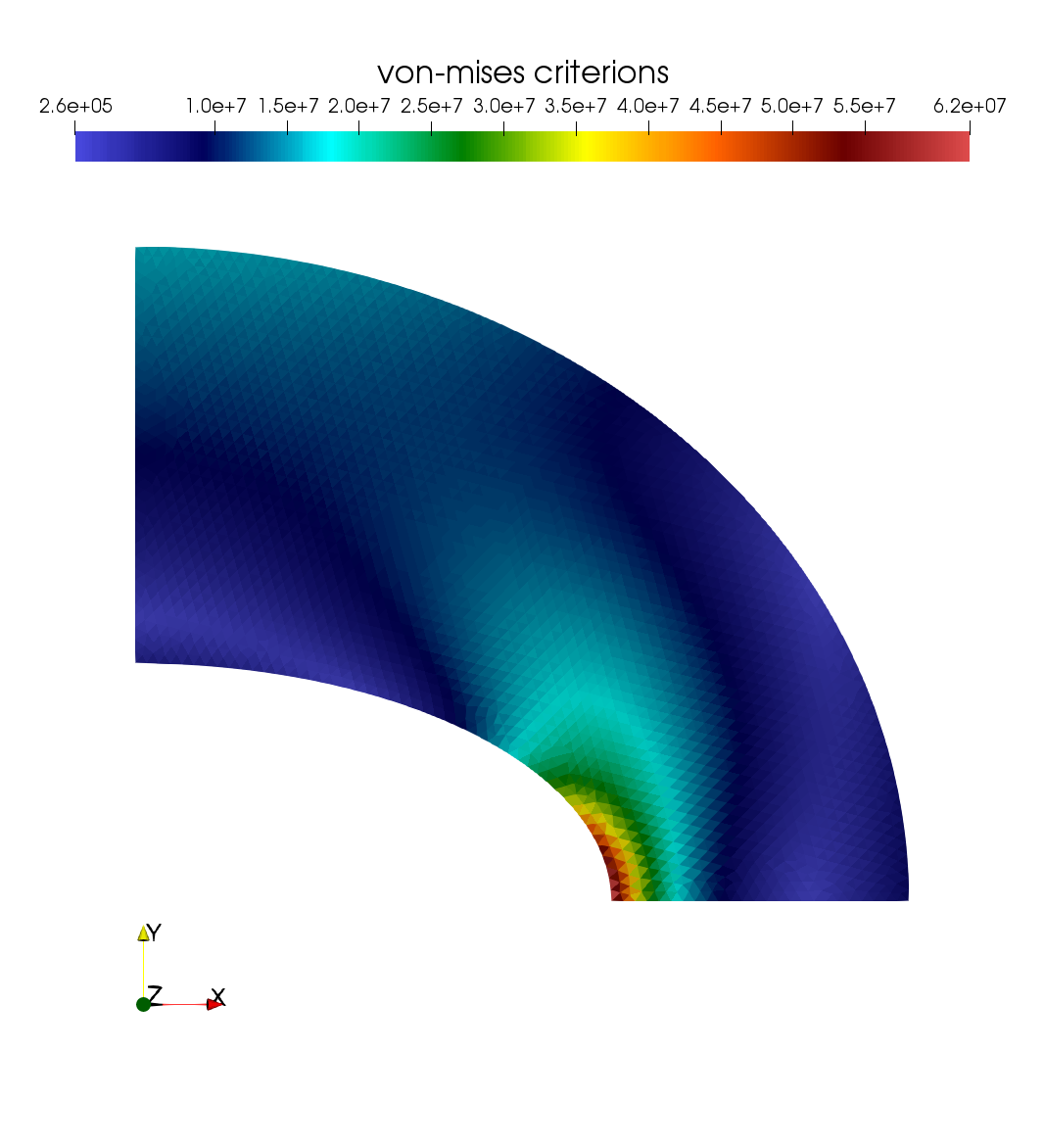
Figure 3. Vonmises