Radiative cavity examples

We simulate radiative heat transfer in 2d and 3d closed cavities. The results of our computations are tested against literature results.

The following tests have been carried out using Newton’s non-linear iterations applied to the non-linear radiative boundary condition (see the heat toolbox documentation for more details on the formulation).

Particular care has been put into the generation of the geometries in order to be as close as possible to the literature examples: small volumes of insulating material are inserted in correspondence of the junctions between the different materials in order to avoid heat trasfer through conduction.

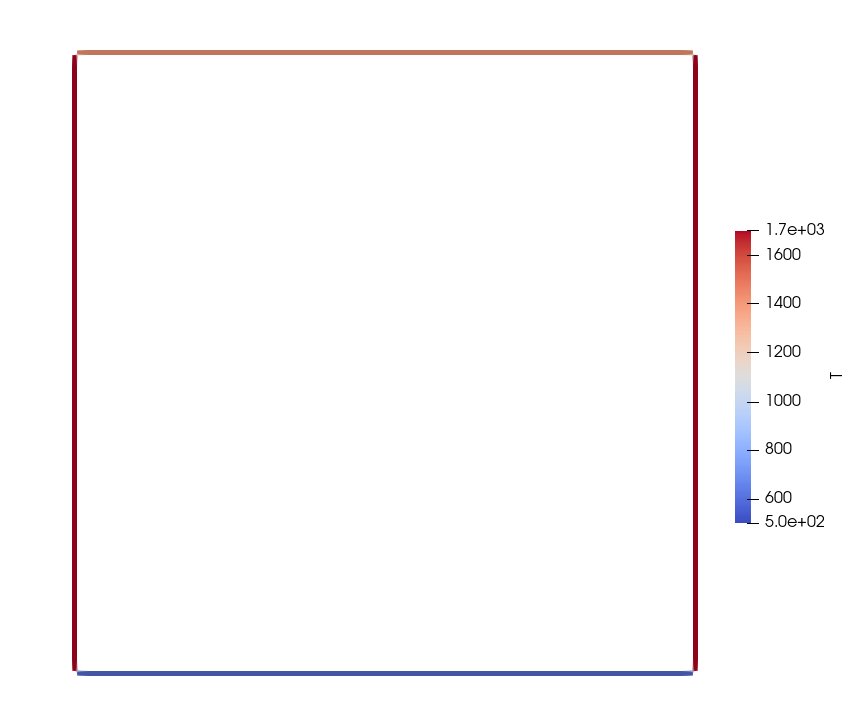
1. Rectangular cavity

This example is taken from [Discontinuous_fem]. It consists in the simulation of the steady state of a rectangular cavity whose surfaces are kept at constant temperatures. The test requires to evalate the net radiative heat flux that leaves each surfaces.

1.1. Geometry and setup

The geometry consists in four rectangles of highly conductive material. They are mutually isolated by small regions of thermal insulator in correspondence of the corners of the cavity.

Figure 1. Geometry of the rectangular cavity

The required temperatures are imposed as Dirichlet boundary conditions on the external surfaces of the rectangles which are parallel to the cavity boundaries. Homogeneous Neumann conditions are imposed on the remaining surfaces of the rectangles.

1.2. Parameters and results

Table 1. Parameters (in SI units)
Name	Value
Heat conductivity rectangles \(k\)	1400
Heat conductivity insulation \(k\)	0.01
Temperature top wall	1400
Temperature side walls	1700
Temperature bottom wall	600
Emissivity \(\epsilon\)	0.5
Length cavity wall \(L\)	3

Table 2. Results (in SI units)
Name	Value
Flux top wall	35767
Flux side walls	-97403
Flux bottom wall	159040

Figure 2. Temperature distribution in the rectangular cavity

2. Triangular cavity

This example is taken from [Comsol]. It consists in the simulation of the steady state of a triangular cavity where heat flux and temperature boundary conditions are imposed. The test requires to evalate the net radiative heat flux and temperatures on the surfaces of the cavity.

2.1. Geometry and setup

The geometry consists in three rectangles of highly conductive material. They are mutually isolated by small regions of thermal insulator in correspondence of the corners of the cavity.

Figure 3. Geometry of the triangular cavity

The required temperatures (fluxes) are imposed as Dirichlet (Neumann) boundary conditions on the external surfaces of the rectangles which are parallel to the cavity boundaries. Homogeneous Neumann conditions are imposed on the remaining surfaces of the rectangles.

Table 3. Parameters (in SI units)
Name	Value
Heat conductivity rectangles \(k\)	400
Heat conductivity insulation \(k\)	0.01
Flux top rectangle	-2000
Flux side rectangle	-1000
Temperature bottom rectangle	300
Emissivity top surface \(\epsilon\)	0.4
Emissivity side surface \(\epsilon\)	0.6
Emissivity bottom surface \(\epsilon\)	0.8

Table 4. Results (in SI units)
Name	Value
Temperature top wall	641
Temperature side wall	600
Flux bottom wall	-2750

Figure 4. Temperature distribution in the triangular cavity

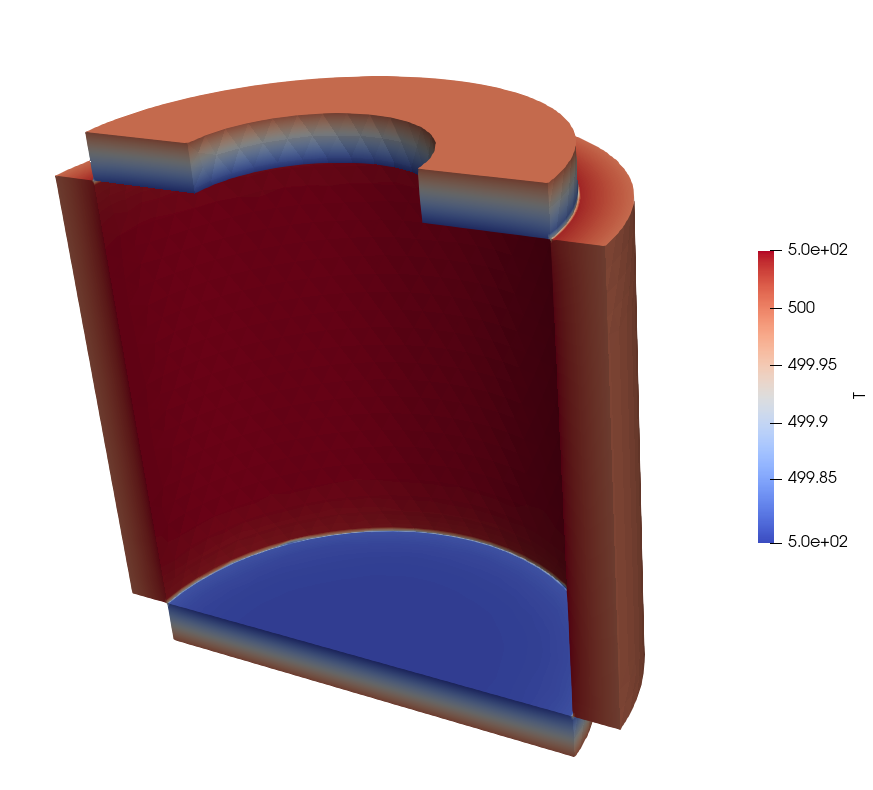
3. Cylindrical cavity

This example is taken from [Radiative_heat_transfer]. It consists in the simulation of the steady state of a cylindrical cavity whose surfaces are kept at constant temperatures. The test requires to evalate the net radiative heat flux that leaves the hole on the top of the cavity.

3.1. Geometry and setup

The geometry consists in three cylinders/annuli of highly conductive material. They are mutually isolated by small regions of thermal insulator in correspondence of the corners of the cavity.

Figure 5. Geometry of the cylindrical cavity (section)

The required temperatures are imposed as Dirichlet boundary conditions on the external surfaces which are parallel to the cavity boundaries. Homogeneous Neumann conditions are imposed on the remaining surfaces.

3.2. Parameters and results

Table 5. Parameters (in SI units)
Name	Value
Heat conductivity rectangles \(k\)	1400
Heat conductivity insulation \(k\)	0.001
Temperature external walls	500
Emissivity \(\epsilon\)	0.5
Cavity diameter	0.5
Top hole diameter	0.25
Height of the cavity	1

Table 6. Results (in SI units)
Name	Value
Flux through hole	88.593

Figure 6. Temperature distribution in the cylindrical cavity (section)

4. Bibliography

[Radiative_heat_transfer] Modest, M.F., Radiative Heat Transfer, Elsevier Science (2013) doi.org/10.1016/C2010-0-65874-3

[Discontinuous_fem] Ben Q. Li, Discontinuous Finite Elements in Fluid Dynamics and Heat Transfer, Springer (2006) doi.org/10.1007/1-84628-205-5

[Comsol] Radiation in a cavity, COMSOL Multiphysics documentation doc.comsol.com/5.6/doc/com.comsol.help.models.heat.cavity_radiation/models.heat.cavity_radiation.pdf