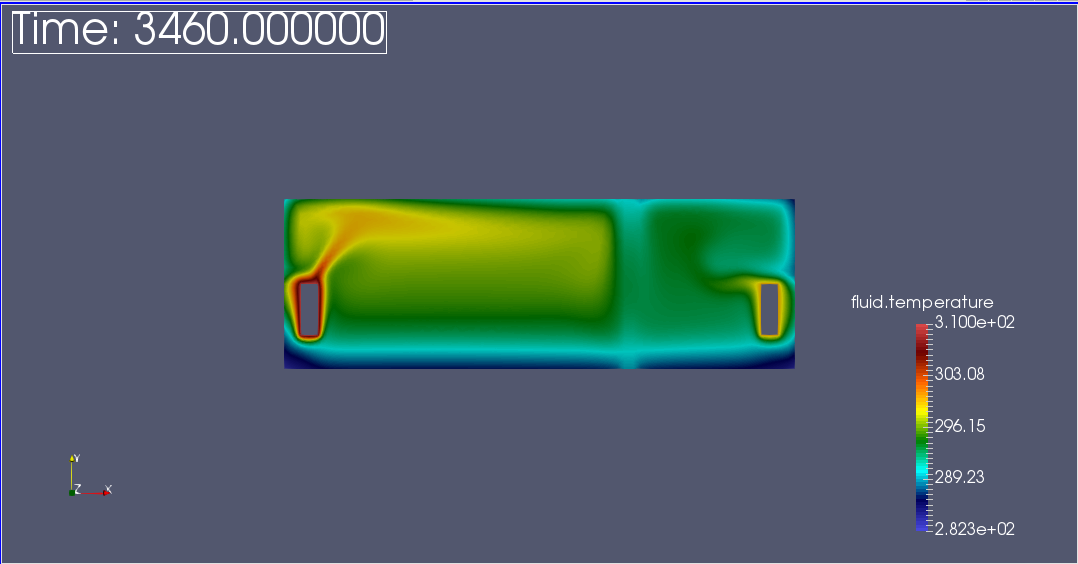
2D building with natural convection

In this example, we simulate the phenomena of natural convection in an apartment of 2 rooms. We use the Navier-Stokes model to simulate the natural convection and the toolbox heatfluid to solve it.

1. Running the case

The command line to run this case is

mpirun -np 8 feelpp_toolbox_heatfluid --case "github:{repo:toolbox,path:examples/modules/heatfluid/examples/2Dbuilding_NS}"
Case option
--case "github:{repo:toolbox,path:examples/modules/heatfluid/examples/2Dbuilding_NS}"

2. Data files

The case data files are available in Github here

3. Model

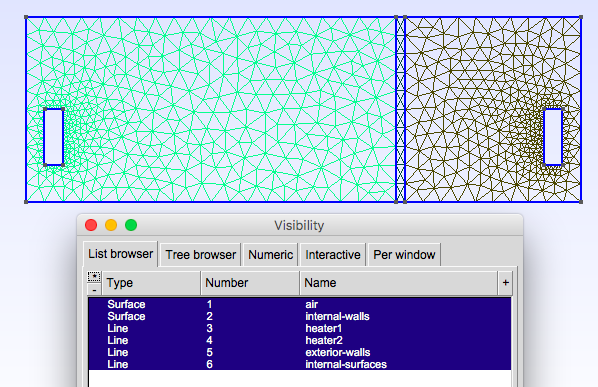
\(\quad\)The 2D thermal model of two parts separated by plaster is considered. It is an object of \(\mathbb{R}^2\), it is subdivided into different domains \(\Omega_i, i = 1,2,3\) (see the image). The sources of heat \(heater_i, i = 1,2\) are the two radiators each of which is located downstairs in each room. The heat \(T\) released in the subdomains is calculated thanks to the equation of heat transfer.

geo
Figure 1. Geometry of \(\Omega = \cup^3_{i=1} \Omega_i\) with \(\partial \Omega = \Gamma_{D} \cup \Gamma_R\)

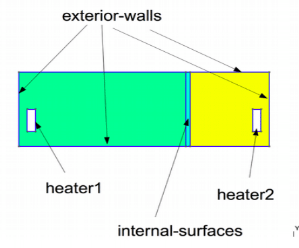
3.1. Boundary condition:

3.1.1. Condition of velocity

On exterior-wall, internal-surfaces, heater1, heater2

\[\mathbb{u} = 0\]

We define the vitess of zero fluid on the walls to assume that there is no circulation of flow in boundary.

3.1.2. Condition of temperature

Condition of Dirichlet

  • On heater1: T= 310 K

  • On heater2: T= 300 K

By fixing the values in two boundary heater1 and heater2, we assure the temperature for two radiators allong the simulation.

Condition de Robin sur exterior-wall
\[-k \nabla T \cdot n = h(T - T_{exp})\]
On the walls

we consider a wall composed of several materials (insulation / plaster / concrete) and an exchange with the outside which is at a temperature of 280 K (\(T_{ext} = 280\)).

As a wall composed of several materials, we have to determine the heat transfer coeffient by the method which is useful to find the heat transfert between simple element such as walls in buidings, within materials. (see [1])

\[\frac{1}{h} = \frac{1}{h_1} + \frac{x}{k} + \frac{1}{h_2}\]

where

  • x = the wall thickness

  • k = the thermal conductivity of materials

  • h = the individual convection heat transfer coefficient for each fluid

    Conditions at the interface \(\Gamma_{ij} = \Omega_i \cap \Omega_j\)
T_i = T_j \\ k_i \nabla T \cdot n_i = - k_j \nabla T \cdot n_j
Initial condition to \(t = 0s\)
\[T = T_0\]

3.2. Input

Table 1. Parameter table
Notation Description Value Unit Note

Paramètres globale

\(t\)

times

s

\(T\)

temperature

\(K\)

\(T_{ext}\)

outside temperature

280

\(K\)

\(T_0\)

initial temperature

280

\(K\)

\(H\)

height

\(1,2,3\)

\(m\)

Air

\(k\)

thermal conductivity

0.03

\(W.m^{-3}.K^{-1}\)

\(\rho\)

mass volumique

1

\( kg/(m^3) \)

\(Cp\)

thermal capacity

1004

\( J/(kg*K) \)

\(h\)

heat transfer coefficient

1.0/(0.06+0.01/0.5 + 0.3/0.8 + 0.20/0.032 +0.016/0.313 +0.14)

\( W.m^{−2}.K^{−1} \)

\(\beta\)

coefficient of thermal expansion

0.003660

\(K^{-1}\)

internal wall

\(k\)

thermal conductivity

0.25

\(W.m^{-3}.K^{-1}\)

\(\rho\)

mass volumique

1

\( kg/(m^3) \)

\(Cp\)

thermal capacity

1000

\( J/(kg*K) \)

\(h\)

heat transfer coefficient

1.0/(0.06+0.01/0.5 + 0.3/0.8 + 0.20/0.032 +0.016/0.313 +0.14)

\( W.m^{−2}.K^{−1} \)

\(\beta\)

coefficient of thermal expansion

0.

\(K^{-1}\)

3.3. Numerical experiences

3.3.1. Geometry

Table 2. Mesh with GMSH

mesh
Parameter to vary
h=0.1;
hHeater=h/5.;

W=2; //height
w=1; //width
ep1=0.1; //plaster width

3.4. Implementation

directory=applications/models/aerothermics/ThermalBuilding/2d

case.dimension=2

[heat-fluid]
mesh.filename=$cfgdir/aero.geo
gmsh.hsize=0.025#0.01#0.02#0.07#0.1
filename=$cfgdir/aero.json

use-natural-convection=1
Boussinesq.ref-temperature=280#293.15

snes-monitor=1
pc-type=lu
ksp-type=preonly

[heat-fluid.heat]
initial-solution.temperature=280#293.15
bdf.order=2

[heat-fluid.fluid]
#solver=Newton #Oseen,Picard,Newton

define-pressure-cst=1
define-pressure-cst.method=algebraic#penalisation#algebraic
define-pressure-cst.markers=air1,air2

bdf.order=2

[ts]
time-step=50#10
time-final=15000
#restart=true
restart.at-last-save=true
#time-initial=0.0002
#save.freq=2
file-format=hdf5
// -*- mode: javascript -*-
{
    "Name": "Thermo dynamics",
    "ShortName":"ThermoDyn",
    "Models":
    {
	"use-model-name":1,
	"fluid":
	{
	    "equations": "Navier-Stokes"
	}
    },
    "Materials":
    {
        "air":
        {
	    "markers":["air1","air2"],
            "physics":["fluid","heat"],
            "rho":"1",
            "mu":"2.65e-2",
            "k":"0.03",
            "Cp":"1004",
            "beta":"0.003660" //0.00006900
        },
        "internal-walls":
        {
	    "markers":"internal-walls",
	    "physics":"heat",
            //"k11":"0.02"//[ W/(m*K) ]
            // //"k11":"0.0262"//[ W/(m*K) ]
            // //"Cp":"1000", //[ J/(kg*K) ]
            // //"rho":"150" //[ kg/(m^3) ]
            "rho":"150",//820,//"82",
            "k":"0.25",//"0.25",
            "Cp":"1000",
            "mu":"1.",//???
            "beta":"0."//"0.003660"//???
        }
    },
    "BoundaryConditions":
    {
        "velocity":
        {
            "Dirichlet":
            {
                "exterior-walls": { "expr":"{0,0}" },
		"internal-surfaces": { "expr":"{0,0}" },
                "heater1": { "expr":"{0,0}" },
                "heater2": { "expr":"{0,0}" }
            }
        },
        "temperature":
        {
            "Dirichlet":
            {
                "heater1": { "expr":"310"/*"330"*/ },
                "heater2": { "expr":"300"/*"320"*/ }
            },
            "Robin":
            {
                "exterior-walls":
                {
                    "expr1":"1.0/(0.06+0.01/0.5 + 0.3/0.8 + 0.20/0.032 +0.016/0.313 +0.14)",// h coeff
                    "expr2":"280"// temperature exterior
                },
		"exterior-walls-nofluid":
                {
                    "expr1":"1.0/(0.06+0.01/0.5 + 0.3/0.8 + 0.20/0.032 +0.016/0.313 +0.14)",// h coeff
                    "expr2":"280"// temperature exterior
                }

            }
        }
    },
    "PostProcess":
    {
	"use-model-name":1,
	"heat-fluid":
	{
	    "Exports":
	    {
		"fields":["fluid.velocity","fluid.pressure","heat.temperature","fluid.pid"]
	    }
	},
	"fluid":
	{
	},
	"heat":
	{
	}
    }
}
Command line to execute
mpirun -np 16 feelpp_toolbox_heatfluid_2d --config-file aero.cfg
Command line to execute using the case with link to folder which represents a remote data in a github repository.
mpirun -np 8 feelpp_toolbox_heat --case "github:{repo:toolbox,path:examples/modules/heatfluid/examples/2Dbuilding_NS}"
Case option
--case "github:{repo:toolbox,path:examples/modules/heatfluid/examples/2Dbuilding_NS}"

You can also use some options to change the variables like time-final, taille du maillage hsize, …​

mpirun -np 8 feelpp_toolbox_heat --case "github:{repo:toolbox,path:examples/modules/heatfluid/examples/2Dbuilding_NS}" --ts.time-final 3000
Case option
--case "github:{repo:toolbox,path:examples/modules/heatfluid/examples/2Dbuilding_NS}"

3.5. Result

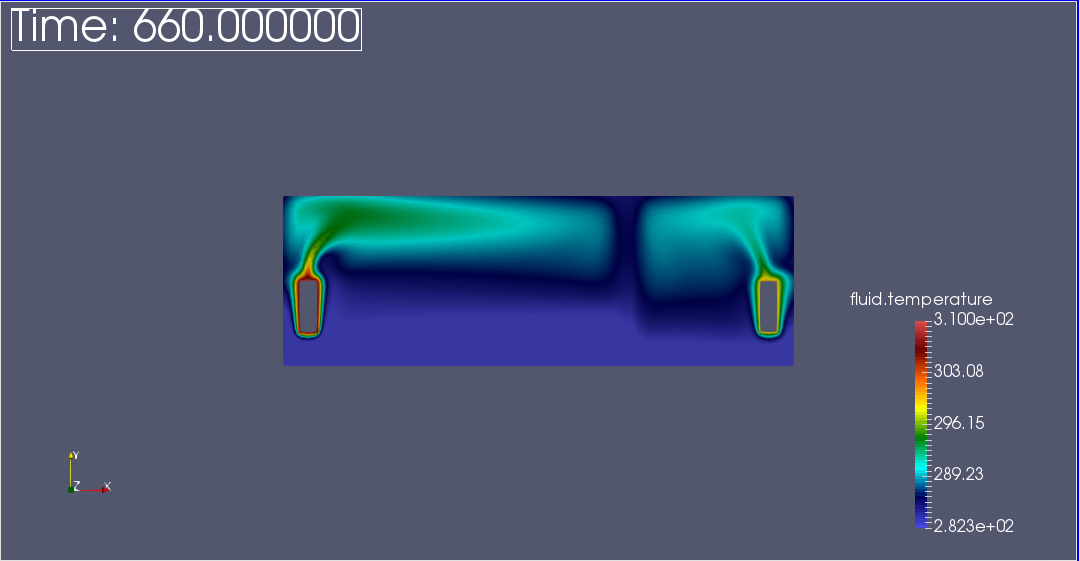
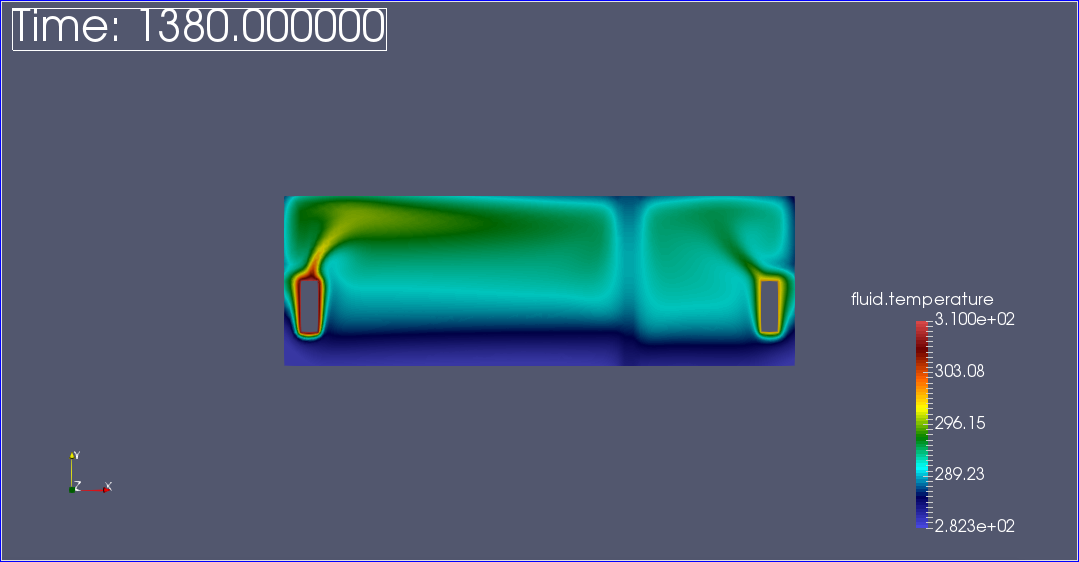
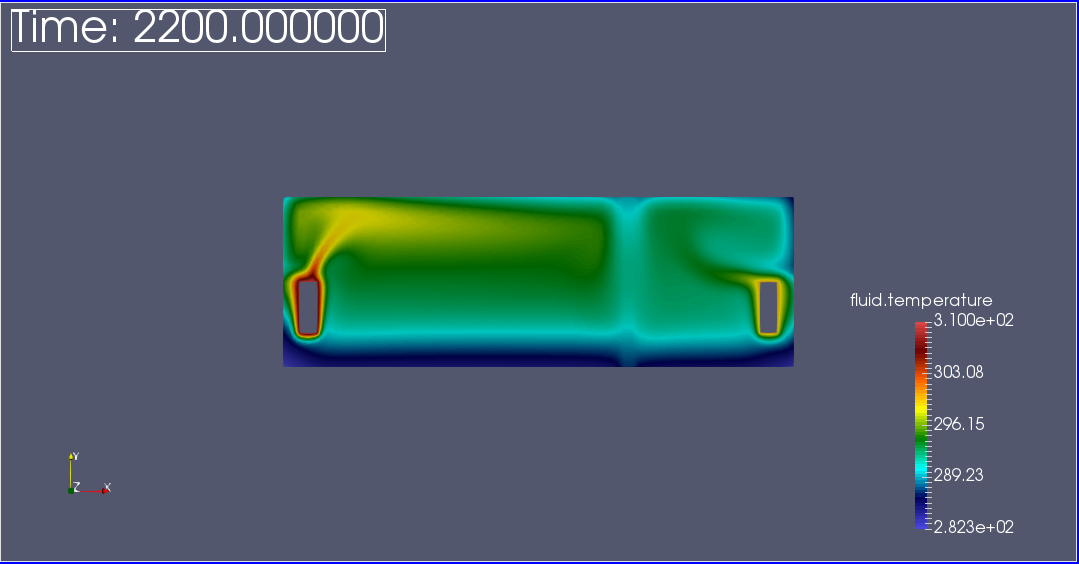
We observe that the flow circulate from the bottom to the top. The cooler fluid in bottom is heated, then becomes less dense and rises. The process continues, forming a convection concurrent and tranfers heat energy around the domain.

Table 3. Heat fluid over times

image1

image2

image3

image4
Average of temperature over times

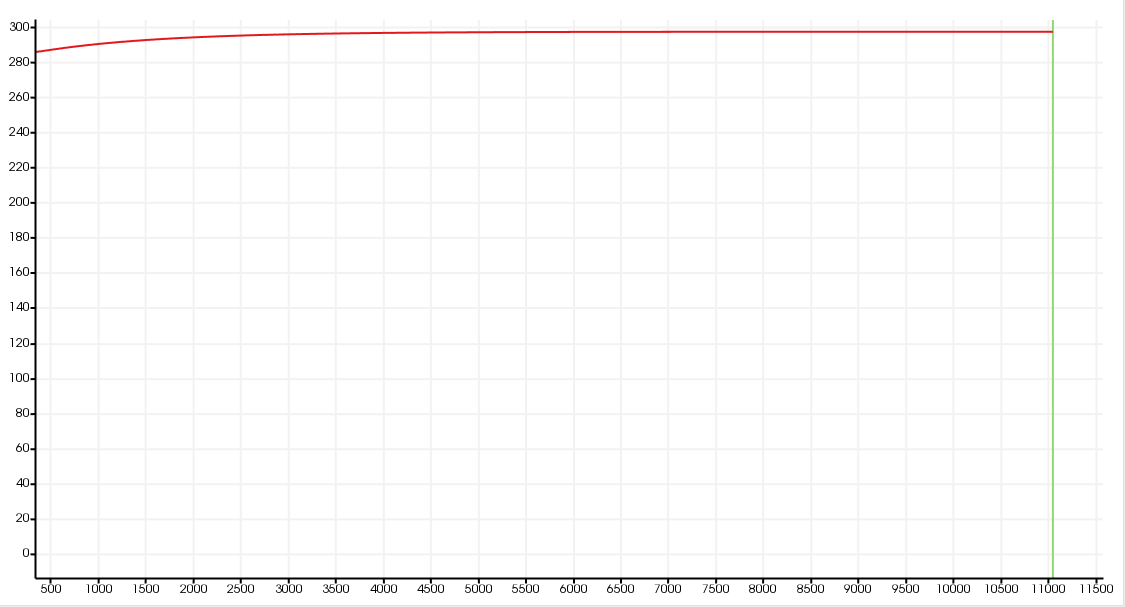
graph1

The graph show the steady state of temperature at 300K in all domains.

Fluid velocity and pressure

velocity a|pressure

The following video shows the transient state of temperature in the domain.

Video of the temperature field in the cabin

Finally we display the 3D interactive results

3.6. Biblio

[1] https://en.wikipedia.org/wiki/Heat_transfer_coefficient