Eléments finis de Lagrange
On va présenter dans ce chapitre le type le plus simple et le plus classique d’éléments finis.
1. Unisolvance
Ceci revient à dire que la fonction :
est bijective.
2. Elément fini de Lagrange
On vérifie aisément que \((p_1,\ldots,p_N)\) ainsi définie forme bien une base de \(P\).
3. Exemples d’éléments finis de Lagrange
3.1. Espaces de polynômes
On notera \(\Pk{k}\) l’espace vectoriel des polynômes de degré total inférieur ou égal à \(k\).
-
Sur \(\RR\), \(\quad\Pk{k}=\hbox{Vect} \{ 1,X,\ldots, X^k\}\quad\) et dim \(\Pk{k}=k+1\).
-
Sur \(\RR^2\), \(\quad\Pk{k}=\hbox{Vect} \{ X^i Y^j ;\quad 0\le i+j \le k\}\quad\) et dim \({ \Pk{k}=\frac{(k+1)(k+2)}{2}}\).
-
Sur \(\RR^3\), \(\quad\Pk{k}=\hbox{Vect} \{ X^i Y^j Z^l ;\quad 0\le i+j+l \le k\}\quad\) et dim \({ \Pk{k}=\frac{(k+1)(k+2)(k+3)}{6}}\).
On notera \(\Qk{k}\) l’espace vectoriel des polynômes de degré inférieur ou égal à \(k\) par rapport à chaque variable.
-
Sur \(\RR\), \(\quad\Qk{k}=\Pk{k}\).
-
Sur \(\RR^2\), \(\quad\Qk{k}=\hbox{Vect} \{ X^i Y^j ; \quad 0\le i,j \le k\}\quad\) et dim \({ \Qk{k}=(k+1)^2}\).
-
Sur \(\RR^3\), \(\quad\Qk{k}=\hbox{Vect} \{ X^i Y^j Z^l ; \quad 0\le i,j,l \le k\}\quad\) et dim \({ \Qk{k}=(k+1)^3}\).
3.2. Exemples 1-D
- Elément \(P_1\)
-
-
\(K=[a,b\)]
-
\(\Sigma=\{a,b\}\)
-
\(P=\Pk{1}\)
-
- Elément \(P_2\)
-
-
\(K=[a,b\)]
-
\({\Sigma=\{a,\frac{a+b}{2},b\}}\)
-
\(P=\Pk{2}\)
-
- Elément \(\Pk{k}\)
-
-
\(K=[a,b\)]
-
\({\Sigma=\{a+i\,\frac{b-a}{k},\quad i=0,\ldots,k\}}\)
-
\(P=\Pk{k}\)
-
3.3. Exemples 2-D triangulaires
- Elément \(\Pk{1}\)
-
-
\(K\)=triangle de sommets \(a_1, a_2, a_3\)
-
\(\Sigma=\{a_1,a_2,a_3\}\)
-
\(P=\Pk{1}\) Les fonctions de base sont définies par \(p_i(a_j)=\delta_{ij}\). Ce sont donc les coordonnées barycentriques : \(p_i=\lambda_i\) (cf annexe [ch:bary]).
-
- Elément \(\Pk{2}\)
-
-
\(K\)=triangle de sommets \(a_1, a_2, a_3\)
-
\(\Sigma=\{a_1,a_2,a_3, a_{12}, a_{13}, a_{23}\}\), où \({a_{ij}=\frac{a_i+a_j}{2}}\).
-
\(P=\Pk{2}\)
-
Les fonctions de base sont \(p_i=\lambda_i (2\lambda_i -1)\) et \(p_{ij}=4\lambda_i\lambda_j\). Un exemple de calcul de ces fonctions de base est donné en annexe [ch:bary].
3.4. Exemples 2-D rectangulaires
- Elément \(\Qk{1}\)
-
-
\(K\)=rectangle de sommets \(a_1, a_2, a_3, a_4\), de côtés parallèles aux axes
-
\(\Sigma=\{a_1,a_2,a_3,a_4\}\)
-
\(P=\Qk{1}\) Les fonctions de base sont \({p_i(X,Y)=\frac{(X-x_j)(Y-y_j)}{(x_i-x_j)(y_i-y_j)}}\), où \((x_i,y_i)\) sont les coordonnées de \(a_i\), et où \(a_j\), de coordonnées \((x_j,y_j)\) est le coin opposé à \(a_i\).
-
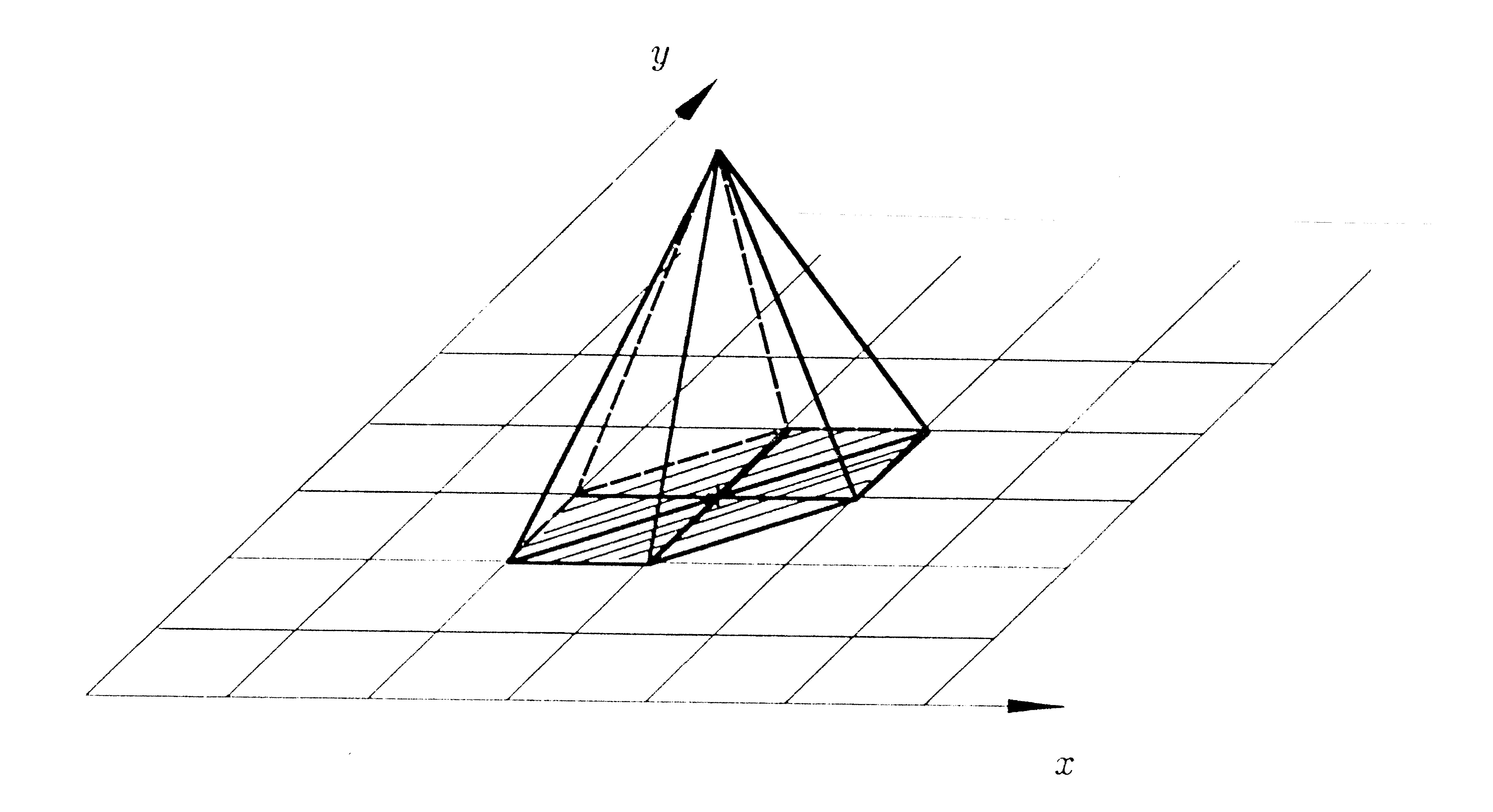
3.5. Exemples 3-D
- Elément tétraèdrique \(\Pk{1}\)
-
-
\(K\)=tétraèdre de sommets \(a_1, a_2, a_3, a_4\)
-
\(\Sigma=\{a_1,a_2,a_3, a_4\}\)
-
\(P=\Pk{1}\)
-
- Elément tétraèdrique \(\Pk{2}\)
-
-
\(K\)=tétraèdre de sommets \(a_1, a_2, a_3, a_4\)
-
\({ \Sigma=\{a_i\}_{1\le i\le 4} \cup \{a_{ij}\}_{1\le i < j \le 4} }\), où \({a_{ij}=\frac{a_i+a_j}{2}}\).
-
\(P=\Pk{2}\)
-
Les fonctions de base sont \(p_i=\lambda_i (2\lambda_i -1)\) et \(p_{ij}=4\lambda_i\lambda_j\).
- Elément parallélépipèdique \(Q_1\)
-
-
\(K\)=parallélépipède de sommets \(a_1, \ldots , a_8\) de côtés parallèles aux axes
-
\(\Sigma=\{a_i\}_{1\le i\le 8}\)
-
\(P=\Qk{1}\)
-
- Elément prismatique
-
-
\(K\)=prisme droit de sommets \(a_1, \ldots , a_6\)
-
\(\Sigma=\{a_i\}_{1\le i\le 6}\)
-
\(P=\{p(X,Y,Z)=(a+bX+cY)+Z(d+eX+fY), \;\; a,b,c,d,e,f \in \RR\}\)
-
4. Famille affine d’éléments finis
| Si l’on est dans \(\RR^n\), \(B\) est donc une matrice \(n\times n\) inversible, et \(b\) est un vecteur de \(\RR^n\). |
D’un point de vue pratique, le fait de travailler avec une famille affine d’éléments finis permet de ramener tous les calculs d’intégrales à des calculs sur l’élément de référence.
Les éléments de référence sont :
-
En 1-D : le segment \([0,1]\)
-
En 2-D triangulaire : le triangle unité, de sommets \((0,0)\), \((0,1)\) et \((1,0)\).
-
En 2-D rectangulaire : le carré unité \([0,1]\times[0,1]\).
-
En 3-D tétraèdrique : le tétraèdre unité, de sommets \((0,0,0)\), \((1,0,0)\), \((0,1,0)\) et \((0,0,1)\).
-
En 3-D parallélépipèdique : le cube unité \([0,1]\times[0,1]\times[0,1]\).
-
En 3-D prismatique : le prisme unité de sommets \((0,0,0)\), \((0,1,0)\), \((1,0,0)\), et \((0,0,1)\), \((0,1,1)\), \((1,0,1)\).
5. Maillages
Nous étendons ici aux dimension 2 et 3 les notions élémentaires de maillage vues en 1D ([sec:constr-du-maill]), voir la figure [fig:2].
On travaille par la suite avec des familles de maillage et on les note \(\set{\mathcal{T}_h}_{h > 0}\).
| Cela veut dire que les élements sont tous de la même taille pour \(h\) donné. |
5.1. Transformation géométrique
Un maillage est généré par
-
un élément de reference noté \(\hat{K}\)
-
une famille de transformations géométriques mappant \(\hat{K}\) vers les éléments \(K_e, e=1,\ldots,\Ne\) dans le maillage
Nous supposerons que ces transformations sont des \(\mathcal{C}^1-\) diffeomorphismes [1].
Afin de spécifier la transformation géométrique, on considère l’élément fini de Lagrange, noté \((\hat{K},\hat{P}_{\mathrm{geo}}, \hat{\Sigma}_{\mathrm{geo}})\), tel que
-
\(\ngeo = \card{\hat{\Sigma}_{\mathrm{geo}}}\)
-
\(\set{\hat{g}_1,\ldots,\hat{g}_{\ngeo}}\) les noeuds de \(\hat{K}\)
-
\(\set{\hat{\psi}_1,\ldots,\hat{\psi}_{\ngeo}}\) les fonctions de forme
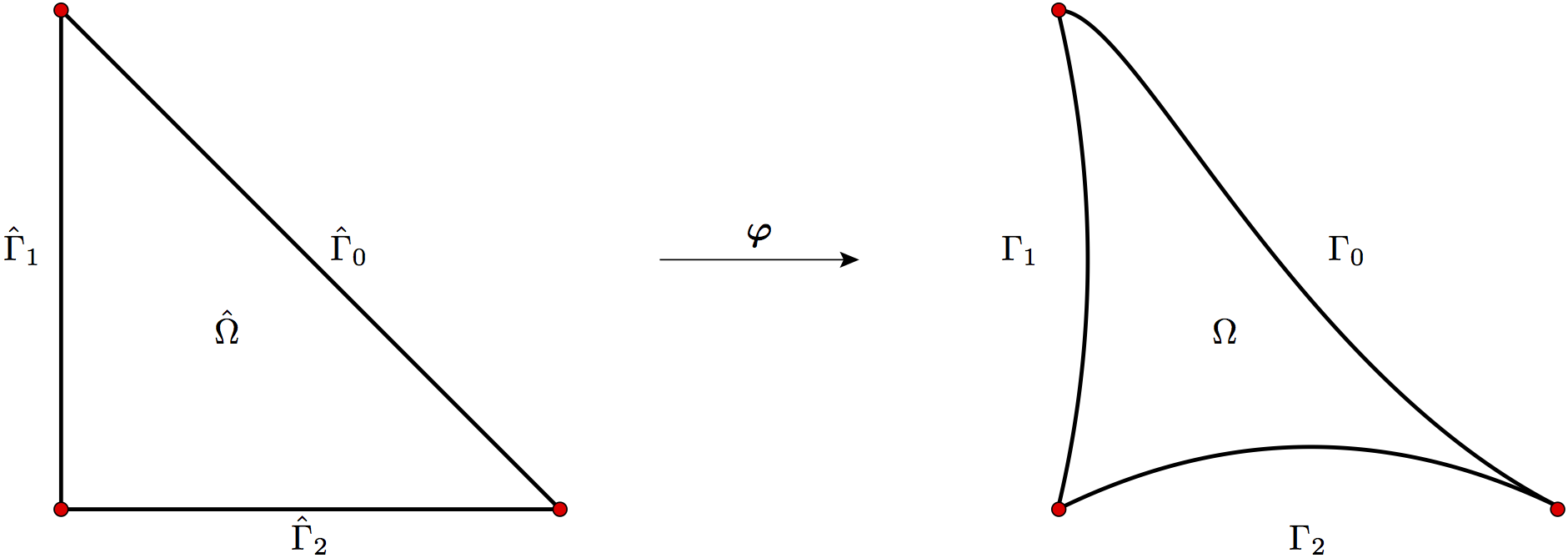
La transformation géométrique est définie comme suit
et en particulier on a
| On a \(T_K \in [\hat{P}_\geo(\hat{K})q\)^d] et que \(\set{g^K_1,\ldots,g^K_\ngeo}\) sont les noeuds géométriques de \(K\). |
\(T_K\) est un \(\mathcal{C}^1\)-diffeomorphism donc la numérotation des noeuds \(\set{g^K_1,\ldots,g^K_\ngeo}\) doit être compatible avec les noeuds de l’élément finit géométrique.
| La numérotation locale des entités géométriques dans \(\hat{K}\) doit être consistente avec la numérotation locale des générateurs de maillage. voir \(\triangleright\) format de fichier Gmsh pour une numérotation locale. |
Un cas particulier est la transformation géométrique affine.
| Si l’élément fini géométrique est \((\hat{K},\poly{P}_1,\Sigma_\ngeo)\) alors les éléments \(K\) sont soit des triangles soit des tétrahèdres. |
Dans Feel++ : Mesh<Simplex<d,1> > ou Mesh<Simplex<d> > est le type pour les maillages affines formés de simplexes dans \(\RR^d\).
|
1 indique l’ordre de l’élément fini géométrique et est la valeur par défaut.
5.2. Quelques calculs avec la transformation géométrique
5.2.1. Gradient, Inverse et Jacobien
On note \(\xi\) un ensemble de \(n\) points dans \(\hat{K}\) et on note \(\nabla T_K(\xi)\) le gradient de \(T_K\) aux points \(\xi\)
et \(B_K(\xi) = \nabla T_K^{-1}(\xi)\) l’inverse du gradient de \(T_K\) aux points \(\xi\) et finalement \(J_K(\xi)\) le jacobien de \(T_K\) en \(\xi\)
5.2.2. Dérivation dans l’élément de référence
Afin de dériver un polynome dans l’élément réel \(K\), grâce à la transformation géométrique et la règle de différentiation des fonctions composées, nous dérivons seulement dans l’élément de référence \(\hat{K}\).
Soit \(f: K \mapsto \RR\) et \(\hat{f}: \hat{K} \mapsto \RR\) telle que \(\hat{f} = f \circ T_K\)
en 2D, on a, en notant \(x=T_K(\xi)\),
5.2.3. Intégration dans l’élément de référence
De manière similaire, au lieu de calculer les intégrales sur l’élément réel \(K\), nous appliquons un changement de variables et calculons les intégrales sur l’élément de réference \(\hat{K}\).
Soit \(f: K \mapsto \RR\) et \(\hat{f}: \hat{K} \mapsto \RR\) telle que \(\hat{f} = f \circ T_K\), et \({\mathbf{F}}: K \mapsto \RR^d\) et \({\hat{\mathbf{F}}}: \hat{K} \mapsto \RR^d\) telle que \(\hat{{\mathbf{F}}} = {\mathbf{F}} \circ T_K\),
On a alors les relations suivantes:
où \({\mathbf{n}}(x)\) est la normale extérieure unitaire à \(\partial K\) évaluée en \(x \in \partial K\), et \({\hat{\mathbf{n}}}(\xi)\) la normale unitaire extérieure à \(\hat{K}\) évaluée en \(\xi \in \partial \hat{K}\).
| Feel++ effectue automatiquement pour vous les changements de variables dans les intégrales. |
| On ne manipule que des maillages conformes dans le cours mais Feel++ peut traiter des maillages non-conformes par exemple dans le contexte de méthode de décomposition de domaines. |
6. Espaces élément fini de Lagrange
Soit \(\mathcal{T}_h\) un maillage généré par \((\hat{K}, \hat{P}_{\mathrm{geo}}, \hat{\Sigma}_{\mathrm{geo}})\), une cellule \(K \in \mathcal{T}_h\) est alors l’image de \(\hat{K}\) par la transformation géométrique \(T_K\) défini par [eq:37].
L’objectif à présent est de générer la famille d’éléments finis de Lagrange grâce à l’élément fini de référence \((\hat{K},\hat{P}, \hat{\Sigma})\)
|
Afin de construire un tel espace on introduit tout d’abord
mais ce n’est pas suffisant: les fonctions \(W_h\) peuvent avoir des sauts entre les éléments du maillage. Nous avons donc besoin d’assurer la continuité de ces fonctions
Concernant l’implémentation, nous avons besoin d’indentifier les degrés de liberté communs entre les éléments quand nous construisons la tables des degrés de liberté.
Voici deux exemples d’espace \(H^1\)-conforme
| espace | d | k=1 | k=2 | k=3 |
|---|---|---|---|---|
\(P_{c,h}^k\) |
2 |
\(N_{so}\) |
\(N_{so}+N_{ar}\) |
\(N_{so}+2N_{ar}+N_{ma}\) |
\(Q_{c,h}^k\) |
2 |
\(N_{so}\) |
\(N_{so}+N_{ar}+N_{ma}\) |
\(N_{so}+2N_{ar}+4N_{ma}\) |
\(P_{c,h}^k\) |
3 |
\(N_{so}\) |
\(N_{so}+N_{ar}\) |
\(N_{so}+2N_{ar}+N_{fa}\) |
\(Q_{c,h}^k\) |
3 |
\(N_{so}\) |
\(N_{so}+N_{ar}+N_{fa}+N_{ma}\) |
\(N_{so}+2N_{ar}+4N_{fa}+8N_{ma}\) |
6.1. Projections orthogonales
On note
les projections orthogonales associées respectivement aux produits scalaires \((u,v)_{0,\Omega} = \int_\Omega u v\) and \((u,v)_{1,\Omega} = \int_\Omega u v + \int_\Omega \nabla u \cdot \nabla v\)
On a pour \(l=1,...,k\) et si \(v \in H^{l+1}(\Omega)\)
Pour calculer \(\Pi^{0,k}_{c,h}\) et \(\Pi^{1,k}_{c,h}\) on a besoin de résoudre les problèmes
| L’opérateur \(\Pi_{\mathrm{c}, b}^{1, k}\) est appelé projecteur elliptique. On peut également considérer la projection orthogonale de \(H_0^1(\Omega)\) dans \(P_{\mathrm{c}, b, 0}^k\) avec le produit scalaire \(\int_{\Omega} \nabla v \cdot \nabla w\). Ce dernier satisfait les mêmes propriétés que celles énoncées ci-dessus pour l’opérateur \(\Pi_{\mathrm{c}, b}^{1, k}\). |
| Des résultats analogues existent pour des opérateurs de projection orthogonale sur les espaces \(Q_{c, b}^k\). |
6.2. Interpolant de Lagrange
| La restriction de l’interpolant de Lagrange à une cellule \(K\) coincide avec l’interpolant de Lagrange appliqué à la fonction dans la cellule \(K\): |
|
Ce théorème est une conséquence directe du théorème d’interpolation local. On notera que l’hypothèse portant sur la régularité de la famille \(\left\{\mathcal{T}_h\right\}_{h>0}\) permet de contrôler uniformément les rapports \(\varpi_K\). Enfin, lorsque la fonction à interpoler n’est pas suffisamment régulière, par exemple si \(v \in H^s\left(\Omega_h\right)\) et \(v \notin H^{s+1}\left(\Omega_h\right)\) pour un entier \(s \in\{1, \ldots, k\}\), l’estimation [eq.62] ci-dessus devient
\[\begin{equation*}
\left\|v-\mathcal{I}_b^{\mathrm{Lag}} v\right\|_{0, \Omega_b}+h\left|v-\mathcal{I}_b^{\mathrm{Lag}} v\right|_{1, \Omega_b} \leqslant c h^s|v|_{s, \Omega_b}
\end{equation*}\]
|
Nous considérons pour cela \(\alpha\) un réel et \(\mathbf{x}=(x_1,...,x_d) \in \mathbb{R}^d\) un point de \(\Omega = [0,1]^d, d=1,2,3\) et \(v\) la fonction définie par
Nous construisons l’interpolant de Lagrange de \(v\) dans \(P^k_{c,h}\) avec \(k=1,...,5\) et \(d=1,2,3\) et étudions l’erreur d’interpolation \(L^2\) et \(H^1\) du théorème [eq:62] en échelle log-log.
Nous devons obtenir des droites de pentes \(k\) (resp. \(k+1\)) pour la norme \(L^2\) (resp. \(H^1\).)
7. Approximation iso-paramétrique
Quand le domaine est courbe, si nous désirons obtenir des propriétés de convergence optimale nous avons besoin de discretiser le bord du domaine avec suffisamment de précision
Notons \((\hat{K},\hat{P}_{\mathrm{geo}}, \hat{\Sigma}_{\geo})\) l’élément fini géométrique et \((\hat{K},\hat{P}, \hat{\Sigma})\) l’élément fini de référence pour \(V_h\).
| Gmsh cite:[gmsh] un mailleur libre permet de générer des maillage d’ordre élevé jusqu’à l’ordre 5 en 2D et 4 en 3D |
| Les résultats sont identiques à ceux du theorème Théorème. |
Nous allons vérifier sur un exemple à l’erreur d’approximation de l’élément géométrique. Considérons les cercles unité généré par une transformation affine, noté \(\Omega^1_h\), et d’ordre 2, noté \(\Omega^2_h\), et calculons leur aire respective.
Construisons une famille de maillage \(\{\calTh\}_{h >0}\), par exemple \(h\in \{0.4, 0.2, 0.1, 0.05\}\) et calculons l’erreur entre le calcul exact de l’aire \(\pi\) et le calcul numérique \(\int_{\Omega^1_h} 1\) et \(\int_{\Omega^2_h} 1\) respectivement.
8. Feel++
En Feel++, un maillage Mesh est décomposé en un ensemble d’éléments décomposés en sous entités (volume,face,arête,point):
-
faces(decomposés en sous entités),
-
arêtes(decomposés en sous entités) et
-
points.
et à chaque élément \(K\) est associé une transformation géométrique \(T_K\).
L’ordre polynomial de la transformation géométrique est donné par le second argument template
Mesh<Simplex<d, k_geo>> (1)
Mesh<Hypercube<d, k_geo>> (2)| 1 | Un maillage de simplexes en dimension \(d\) avec transformation géométrique d’ordre \(k_{\mathrm{geo}}\). |
| 2 | Un maillage d’hypercubes en dimension \(d\) avec transformation géométrique d’ordre \(k_{\mathrm{geo}}\). |
Ain de parcourir les éléments et faces du maillage, Feel++ fournit des fonctions renvoyant des itérateurs (début et fin) sur ces ensembles
elements(mesh)-
retourne 2 itérateurs sur l’ensemble des éléments du maillage
markedelements(mesh,<int>)etmarkedelements(mesh,<string>)-
retourne 2 itérateurs sur les éléments marqués par l’entier
<int>et la chaîne des caractères<string>respectivement, cela correspondra typiquement à des propriétés de matériau boundaryfaces(mesh)-
retourne 2 itérateurs sur les faces au bord du maillage
markedfaces(mesh,<int>)etmarkedelements(mesh,<string>)-
retourne 2 itérateurs sur les faces marquées par l’entier
<int>et la chaîne des caractères<string>respectivement, cela correspondra typiquement aux conditions aux limites
| TODO : link pending to Feel++ user manual mesh iterators section. |
L’espace d’approximation \(V_h\) \(H^1\)-conforme (espaces de fonctions continues sur \(\Omega\) polynomiales par morceaux de degré \(\leq k\)) est défini comme suit
FunctionSpace<Mesh<Simplex<d, k_geo> >, bases<Lagrange<k> > > V_h; (1)
FunctionSpace<Mesh<Hypercube<d, k_geo> >, bases<Lagrange<k> > > V_h; (2)| 1 | \(\Pch{k}\) |
| 2 | \(\Qch{k}\) |
9. Du problème global aux éléments locaux
On va maintenant faire le lien entre la résolution d’un problème par méthode d’éléments finis et les notions qui viennent d’être introduites.
Soit une EDP à résoudre sur un domaine \(\Omega\), et \(V\) l’espace de Hilbert dans lequel on cherche une solution de la formulation variationnelle du problème.
On réalise un maillage de \(\Omega\) par une famille affine de \(N_e\) éléments finis \((K_i,\Sigma_i,P_i)_{i=1,\ldots,N_e}\).
Par unisolvance, la solution approchée \(u_h\) sera entièrement définie sur chaque élément \((K_i,\Sigma_i,P_i)\) par ses valeurs sur les points de \(\Sigma_i\), qu’on appellera les noeuds du maillage.
Il est à noter qu’un noeud sera en général commun à plusieurs éléments adjacents.
Le nombre total de noeuds \(N_h\) est donc inférieur à \(N_e\times\hbox{Card} \Sigma_i\), et on a dim \(V_h = N_h\).
Notons \(a_1,\ldots,a_{N_h}\) les noeuds du maillage.
Le problème approché se ramène donc à la détermination des valeurs de \(u_h\) aux points \(a_i\): ce sont les degrés de liberté du problème approché.
On va construire une base de \(V_h\) en associant à chaque ddl \(a_i\) un vecteur de la base. On définit ainsi les fonctions de base globales \(\varphi_i\) (\(i=1,\ldots,N_h\)) par
L’espace d’approximation interne est donc alors :
| On remarque qu’une telle fonction \(\varphi_i\) est nulle partout, sauf sur les éléments dont \(a_i\) est un noeud. |
En effet, si \(a_i\) n’appartient pas à un élément \(K\), \(\varphi_i\) est nulle sur tous les noeuds de \(K\), et donc sur \(K\) tout entier par unisolvance.
De plus, sur un élément \(K\) dont \(a_i\) est un noeud, \(\varphi_i\) vaut 1 sur \(a_i\) et 0 sur les autres noeuds de \(K\).
Donc \(\varphi_i\, _{|K}\) est une fonction de base locale de \(K\).
| la fonction de base globale \(\varphi_i\) est donc construite comme la réunion des fonctions de base locales sur les éléments du maillage dont \(a_i\) est un noeud. |
C’est à ce niveau que se situe le lien entre les définitions locales introduites au Elément fini de Lagrange et le problème global approché à résoudre.
Par ailleurs, ceci implique que tous les calculs à effectuer sur les fonctions de base globales peuvent se ramener à des calculs sur les fonctions de base locales, et donc simplement à des calculs sur l’élément de référence (car on a maillé le domaine avec une famille d’éléments finis affine-équivalents).
|
Maillage non conforme
Ce type de définition des fonctions de base n’est possible que si le maillage est conforme, c’est à dire si l’intersection entre deux éléments est soit vide, soit réduite à un sommet ou une arête en dimension 2 (ou à un sommet, une arête ou une face en dimension 3). On interdit ainsi les situations du type de celle de la figure. |
10. Exercices
-
Calculer les fonctions de base locales des éléments finis de Lagrange introduits dans ce chapitre.
-
Donner l’allure des fonctions de base globales correspondantes. Sont-elles continues ? dérivables ?
-
Pour les éléments finis de Lagrange introduits dans ce chapitre, écrire le changement de variable affine entre élément quelconque et élément de référence.
 .pdf
.pdf