Théorèmes intégraux en calcul vectoriel

Nous sommes maintenant prêts à relier le calcul vectoriel différentiel et le calcul vectoriel intégral. Cela se fera au moyen des importants théorèmes de Green, Gauss et Stokes.

Les théorèmes intégraux de base de l’analyse vectorielle trouvent leur origine dans les applications.

Le théorème de Green, découvert vers 1828, est apparu en relation avec la théorie du potentiel (cela inclut les potentiels gravitationnels et électriques). Le théorème de Gauss - le théorème de divergence - est lié à l’étude de la capillarité (ce théorème doit être attribué conjointement au mathématicien russe Ostrogradsky, qui a découvert le théorème à peu près au même moment que Gauss). Le théorème de Stokes a été suggéré pour la première fois dans une lettre adressée à Stokes par le physicien Lord Kelvin en 1850 et a été utilisé par Stokes lors de l’examen pour le prix Smith en 1854

1. Formule de Green

Utilisons la notation \(\partial D\) pour la courbe orientée \(C^{+}\), c’est-à-dire la courbe du bord de \(D\) orientée dans le sens inverse des aiguilles d’une montre. Nous pouvons écrire le théorème de Green comme

\[\int_{\partial D} P d x+Q d y=\iint_{D}\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) d x d y\]

avec \(P,Q: (x,y) \in D \mapsto \mathbf{R}\),

\[\int_{\partial D} P d x+Q d y = \int_{\partial D} \left( P(x(t),y(t)) x'(t) + Q(x(t),y(t)) y'(t) \right) dt\]

et \(t\) est la variable de la paramétrisation \(t \mapsto ( x(t), y(t) )\) de \(\partial D\).

Le théorème de Green est très utile car il relie une intégrale de ligne autour du bord d’une région à une intégrale de surface sur l’intérieur de la région, et dans de nombreux cas, il est plus facile d’évaluer l’intégrale de ligne que l’intégrale de surface et vice versa. Par exemple, si nous savons que \(P\) s’annule sur \(\partial D\), nous pouvons immédiatement conclure que \(\iint_{D}(\partial P / \partial y) d x d y=0\) bien que \(\partial P / \partial y\) peut ne pas s’annuler sur l’intérieur.

1.1. Application: Aire d’une Région

Nous pouvons utiliser le théorème de Green pour obtenir une formule pour l’aire d’une région délimitée par une simple courbe fermée.

Théorème: Aire d’une région

Si \(C\) est une simple courbe fermée qui délimite une région à laquelle s’applique le théorème de Green, alors l’aire de la région \(D\) délimitée par \(C=\partial D\) est

\[A=\frac{1}{2} \int_{\partial D} x d y-y d x\]

1.2. Forme Vectorielle utilisant la divergence

Il existe une autre forme de théorème de Green qui peut être généralisée à \(\mathbb{R}^{3}\).

Théorème: Divergence Theorem in the Plane

Soit la \(D \subset \mathbb{R}^{2}\) une région à laquelle s’applique le théorème de Green et soit \(\partial D\) sa limite. Soit \(n\) la normale unitaire extérieure à \(\partial D.\) Si \(\mathbf{c} : [a, b] \rightarrow \mathbb{R}^{2}, t \mapsto \mathbf{c}(t)=(x(t), y(t))\) est à paramétrage orienté positivement de \(\partial D, \mathbf{n}\) est donnée par

\[\mathbf{n}=\frac{\left(y^{\prime}(t),-x^{\prime}(t)\right)}{\sqrt{\left[x^{\prime}(t)\right]^{2}+\left[y^{\prime}(t)\right]^{2}}}\]

(voir Figure ci-dessous ). Soit \(\mathbf{F}=P \mathbf{i}+Q \mathbf{j}\) un champ de vecteurs \(C^{1}\) sur \(D\). Alors

\[\int_{\partial D} \mathbf{F} \cdot \mathbf{n} d s=\iint_{D} \operatorname{div} \mathbf{F} d A\]

Figure 1. \(\mathbf{n}\) est la normale unitaire extérieure à \(\partial D\)

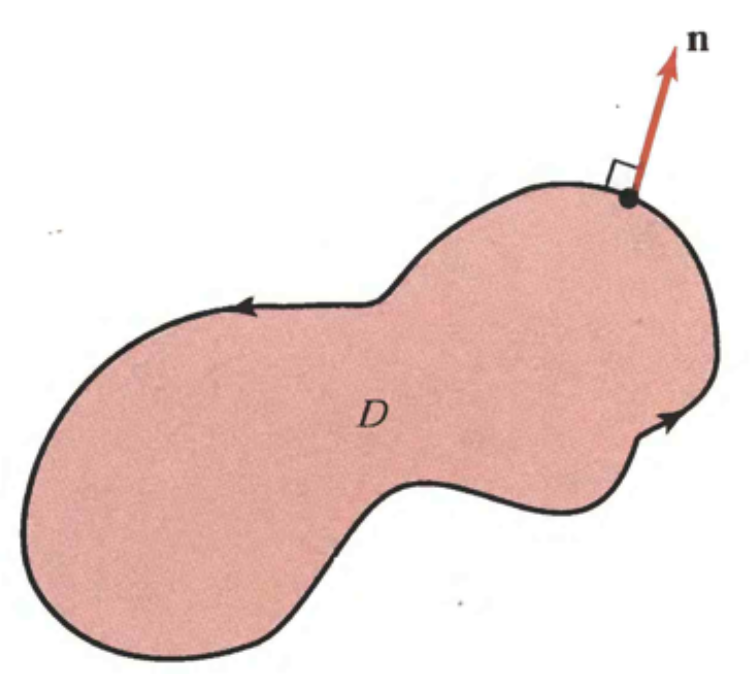
Soit \(\Omega\) un ouvert non vide de \(\mathbb{R}^d\), notons \(\partial\Omega\) son bord. Notons \(\mathbf{n}\) normal extérieure unitaire locale à \(\partial\Omega\).

Nous avons les propriétés suivantes appelées Formules de Green qui sont simplement des extensions de l’intégration par parties. Soit \(\mathbf{e}_k\) le vecteur unitaire dans la direction \(x_k\), \(u,v\) 2 champs scalaires et \(\mathbf{E}\) un champ de vecteurs:

\[\int_\Omega \frac{\partial u}{\partial x_k}\; v\; dx = - \int_\Omega u \; \frac{\partial v}{\partial x_k} \; dx + \int_{\partial \Omega} u\, v \; (\mathbf{e}_k \cdot \mathbf{n})\; ds\]

\[\int_\Omega \Delta u \; v\; dx = - \int_\Omega \nabla u \cdot \nabla v \; dx + \int_{\partial \Omega} \frac{\partial u}{\partial n}\, v \; ds\]

\[\int_\Omega u \; \nabla \cdot \mathbf{E} \; dx = - \int_\Omega \nabla u \cdot \mathbf{E} \; dx + \int_{\partial \Omega} u \; (\mathbf{E} \cdot \mathbf{n})\; ds\]