Manipulate Expressions
We start with setting the Feel++ environment and loading the Feel++ library.
import feelpp
import sys
app = feelpp.Environment(["myapp"],config=feelpp.localRepository(""))1. Create and evaluate expressions
An expression is a mathematical expression that can be evaluated at a given point and depend on multiple variables. It can be a scalar, a vectorial or a matricial expression. The expression can be created from a string. The expression can be then evaluated at a given point.
1.1. Scalar expression
expr = feelpp.expr("x+y:x:y") (1)
expr.evaluate({"x":1,"y":2}) (2)| 1 | Create a scalar expression from a string, the symbols are listed at the end of the string using : as separator. |
| 2 | Evaluate the expression at the point (1,2), it returns a array with one element. |
Results
array([3.])
The expression can also be evaluated at a set of points.
expr.setParameterValues({"y":2}) (1)
import numpy as np
x=np.linspace(0,1,10) (2)
expr.evaluate("x",x) (3)| 1 | Set the value of the parameter y to 2 |
| 2 | Create a numpy array with 10 points between 0 and 1 |
| 3 | Evaluate the expression at the 10 equidistributed points between 0 and 1, it returns a array with two elements. |
Results
array([2. , 2.11111111, 2.22222222, 2.33333333, 2.44444444,
2.55555556, 2.66666667, 2.77777778, 2.88888889, 3. ])
1.2. Vectorial expression
We start with an expression that depends on two variables x and y and create a vectorial expression with the expression x and y.
expr21 = feelpp.expr("{x,y}:x:y",row=2,col=1) (1)
expr21.evaluate({"x":1,"y":2}) (2)| 1 | Create a vectorial expression from a string, the symbols are listed at the end of the string using : as separator. |
| 2 | Evaluate the expression at the point (1,2), it returns a array with two elements. |
Results
array([1., 2.])
Now we turn to a vectorial expression with 3 components.
expr31 = feelpp.expr("{x,y,z+x}:x:y:z",row=3,col=1) (1)
expr31.evaluate({"x":1,"y":2,"z":10}) (2)| 1 | Create a vectorial expression from a string, the symbols are listed at the end of the string using : as separator. |
| 2 | Evaluate the expression at the point (1,2,10), it returns a array with three elements. |
Results
array([ 1., 2., 11.])
1.3. Matricial expression
We start with a 2x2 matricial expression.
expr22 = feelpp.expr("{x+y,x,y,y-x}:x:y", row=2, col=2) (1)
expr22.evaluate({"x":1,"y":2}) (2)| 1 | Create a matricial expression from a string, the symbols are listed at the end of the string using : as separator. |
| 2 | Evaluate the expression at the point (1,2), it returns a array with four elements. |
Results
array([[3., 1.],
[2., 1.]])
We now turn to a 3x3 matricial expression.
expr33 = feelpp.expr("{x,y,z,x-y,y-y,z+x+y,z,y,x}:x:y:z",row=3,col=3) (1)
expr33.evaluate({"x":1,"y":2,"z":3}) (2)| 1 | Create a matricial expression from a string, the symbols are listed at the end of the string using : as separator. |
| 2 | Evaluate the expression at the point (1,2,3), it returns a array with nine elements. |
Results
array([[ 1., 2., 3.],
[-1., 0., 6.],
[ 3., 2., 1.]])
2. Differentiation
The member functions diff and diff2 allows to compute the first and second symbolic derivatives of a function. The first argument is the symbol with respect to which the derivative is computed.
ex=feelpp.expr("a*sin(x):x:a")
ex.setParameterValues({"a":1})
exd = ex.diff("x") (1)
exd2 = ex.diff2("x") (2)
exda = ex.diff("a") (3)
exdax = ex.diff("a").diff("x") (4)
x=np.linspace(0,2*math.pi,200)
print(f" ex: {ex}")
print(f" exd: {exd}")
print(f" exd2: {exd2}")
print(f" exda: {exda}")
print(f"exdaa: {exdax}")| 1 | First derivative with respect to x\(\frac{\partial \cdot }{\partial x}\) |
| 2 | Second derivative with respect to x\(\frac{\partial^2 \cdot }{\partial^2 x}\) |
| 3 | First derivative with respect to a \(\frac{\partial \cdot }{\partial a}\) |
| 4 | First derivative with respect to a and then with respect to x \(\frac{\partial^2 \cdot}{\partial x \partial a}\) |
Results
ex: sin(x)*a exd: a*cos(x) exd2: -sin(x)*a exda: sin(x) exdax: cos(x)
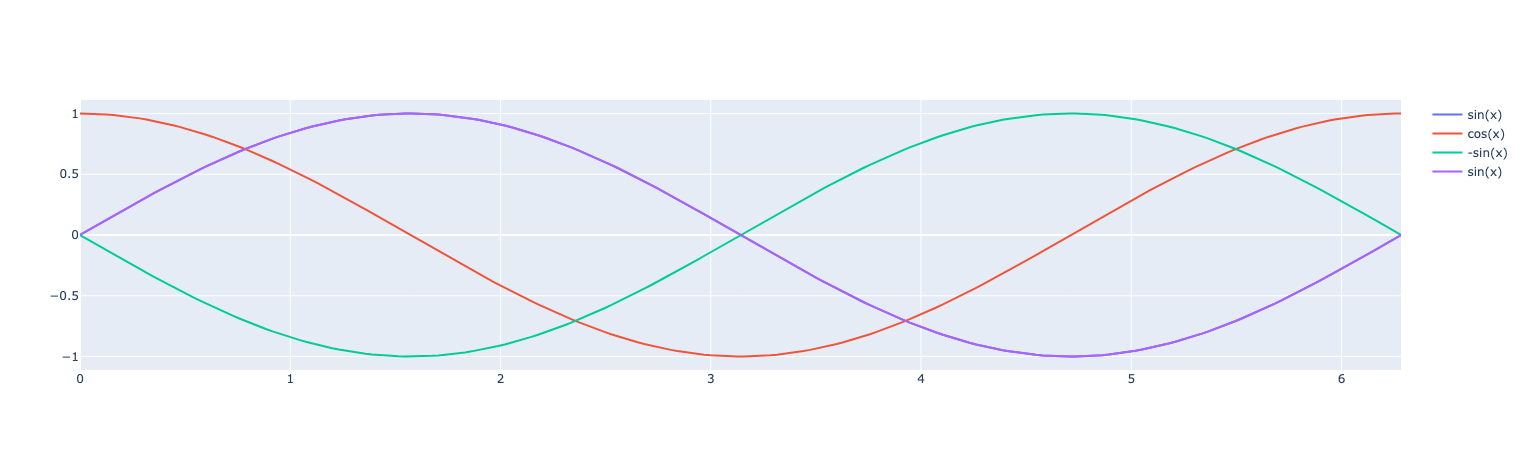
Now let’s plot the expression and its derivative. The first and last are the same.
import plotly.graph_objects as go
fig = go.Figure()
fig.add_trace(go.Scatter(x=x, y=ex.evaluate("x",x), name="sin(x)"))
fig.add_trace(go.Scatter(x=x, y=exd.evaluate("x",x), name="cos(x)"))
fig.add_trace(go.Scatter(x=x, y=exd2.evaluate("x",x), name="-sin(x)"))
fig.add_trace(go.Scatter(x=x, y=exda.evaluate("x",x), name="sin(x)"))
fig.show()Results
2.1. Derivative of a vectorial expression
Here is an example of a vectorial expression and its derivative with respect to x and y.
expr21 = feelpp.expr("{x^3,x*y^2}:x:y", row=2, col=1) (1)
print("d(x,y)/dx = ",expr21.diff("x")) (2)
print("d(x,y)/dy = ", expr21.diff("y")) (3)
print("d2(x,y)/dxdy = ", expr21.diff("x").diff("y")) (4)
print("d2(x,y)/dydx = ", expr21.diff("y").diff("x")) (5)| 1 | Create a vectorial expression from a string, the symbols are listed at the end of the string using : as separator. |
| 2 | First derivative with respect to x\(\frac{\partial \cdot }{\partial x}\) |
| 3 | First derivative with respect to y\(\frac{\partial \cdot }{\partial y}\) |
| 4 | First derivative with respect to x and then with respect to y \(\frac{\partial^2 \cdot}{\partial x \partial y}\) |
| 5 | First derivative with respect to y and then with respect to x \(\frac{\partial^2 \cdot}{\partial y \partial x}\) |
Results
d(x,y)/dx = [[3*x^2],[y^2]] d(x,y)/dy = [[0],[2*x*y]] d2(x,y)/dxdy = [[0],[2*y]] d2(x,y)/dydx = [[0],[2*y]]
| similar results are obtained for matricia expressions. |
3. Special functions
The Feel++ library provides a set of special functions that can be used in expressions.
3.1. function with multiple parameters
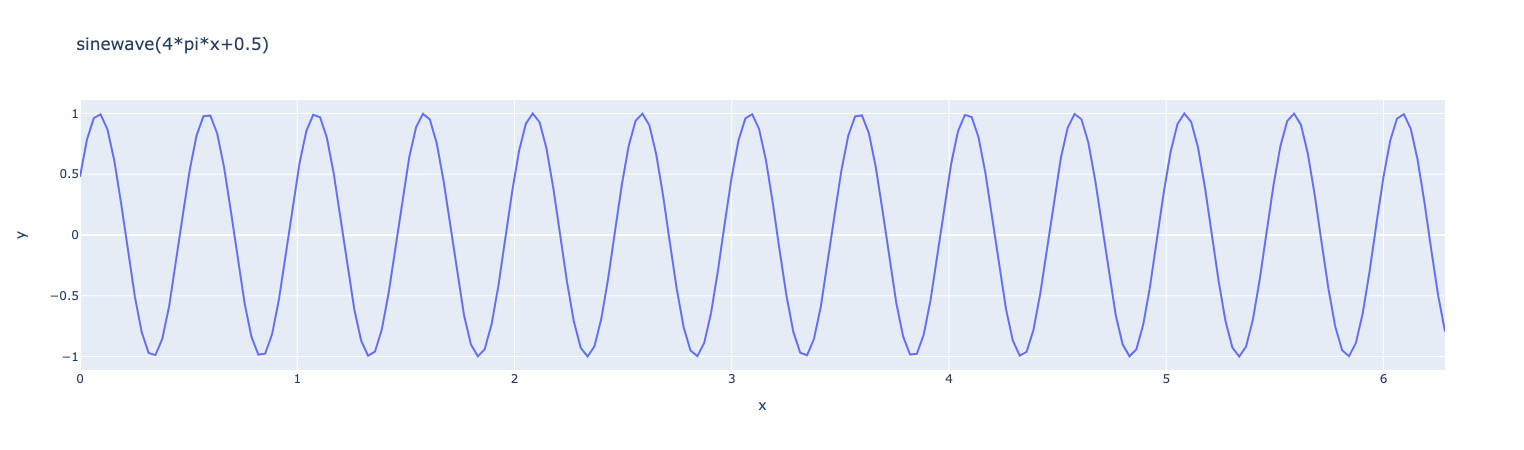
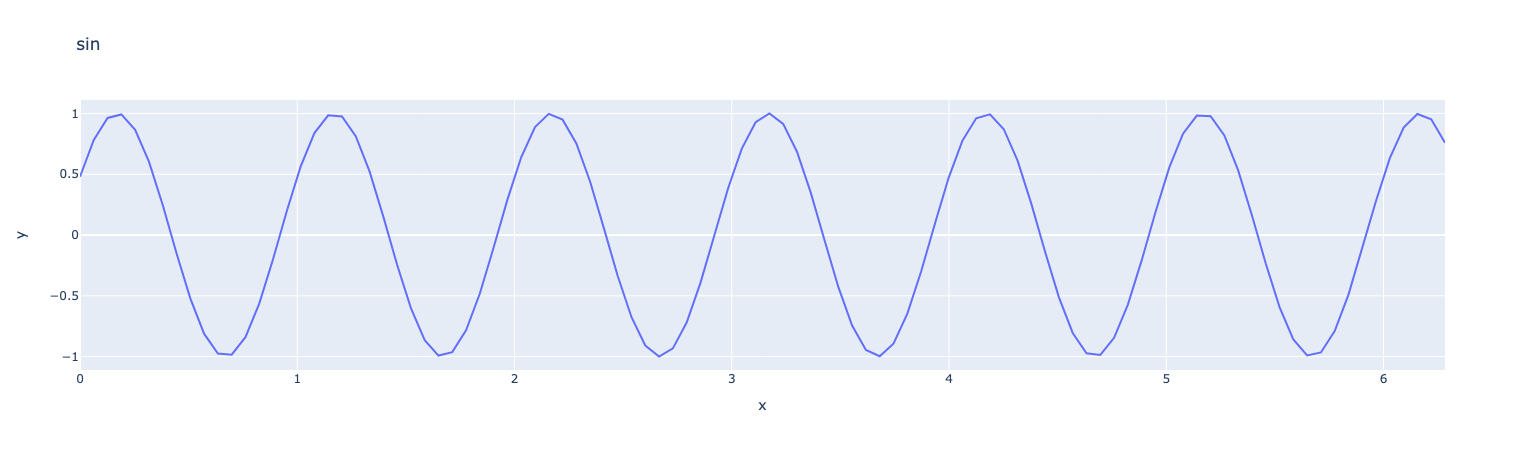
ex=fpp.expr("sin(w*x+b):x:w:b")
ex.setParameterValues({"w":2*math.pi,"b":0.5})
x=np.linspace(0,2*math.pi,100)
y=ex.evaluate("x",x)
fig = px.line(x=x, y=y, title="sin",labels={"x":"x","y":r'y'})
fig.show()Results
3.2. clamp
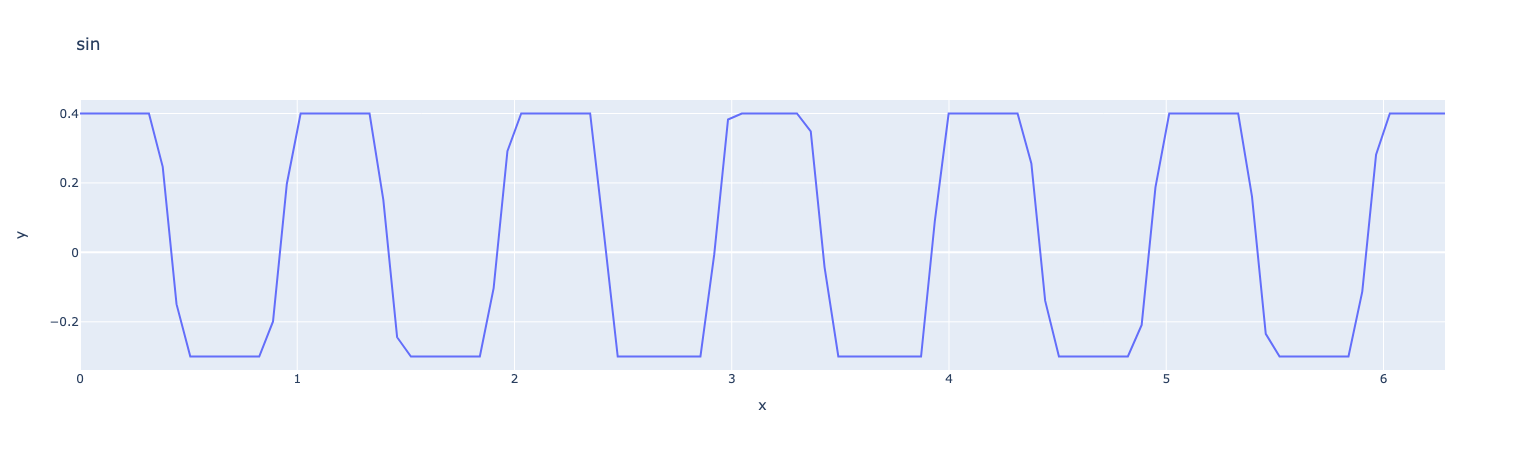
The function clamp allows to clamp a value between two bounds.
ex=fpp.expr("clamp(sin(w*x+b),-0.3,0.4):x:w:b")
ex.setParameterValues({"w":2*math.pi,"b":0.5})
x=np.linspace(0,2*math.pi,100)
y=ex.evaluate("x",x)
fig = px.line(x=x, y=y, title="f",labels={"x":"x","y":r'y'})
fig.show()Results
3.3. mapabcd
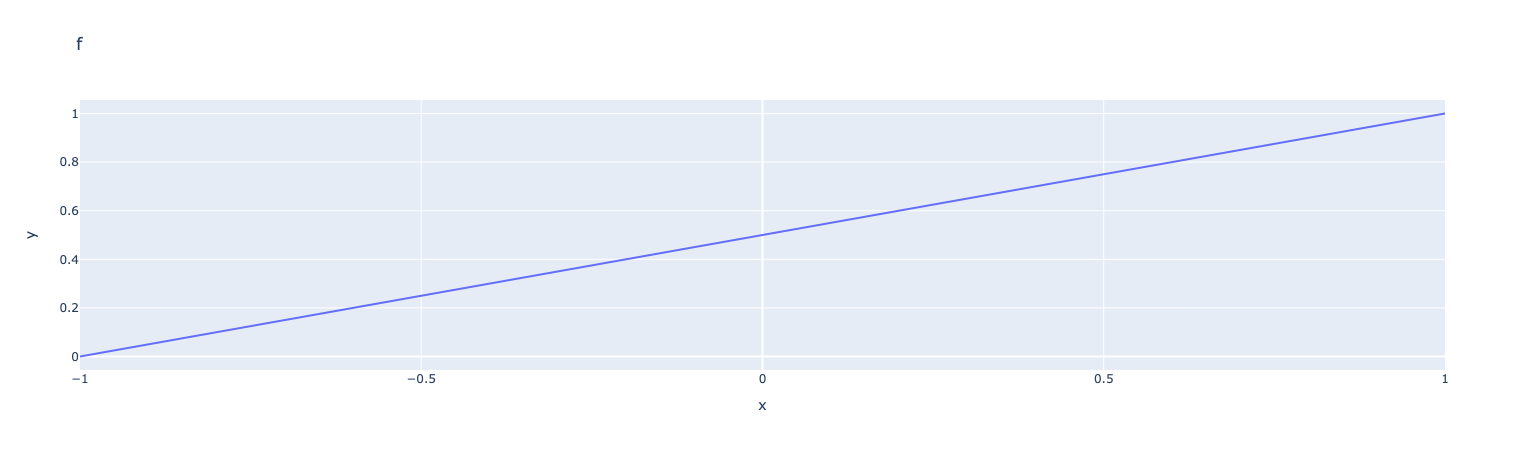
The function mapabcd allows to map a value from a given interval to another interval. The first argument is the value to map, the second and third arguments are the lower and upper bounds of the interval to map from, the fourth and fifth arguments are the lower and upper bounds of the interval to map to.
ex=fpp.expr("mapabcd(x,-1,1,0,1):x")
x=np.linspace(-1,1,100)
y=ex.evaluate("x",x)
fig = px.line(x=x, y=y, title="f",labels={"x":"x","y":r'y'})
fig.show()Results
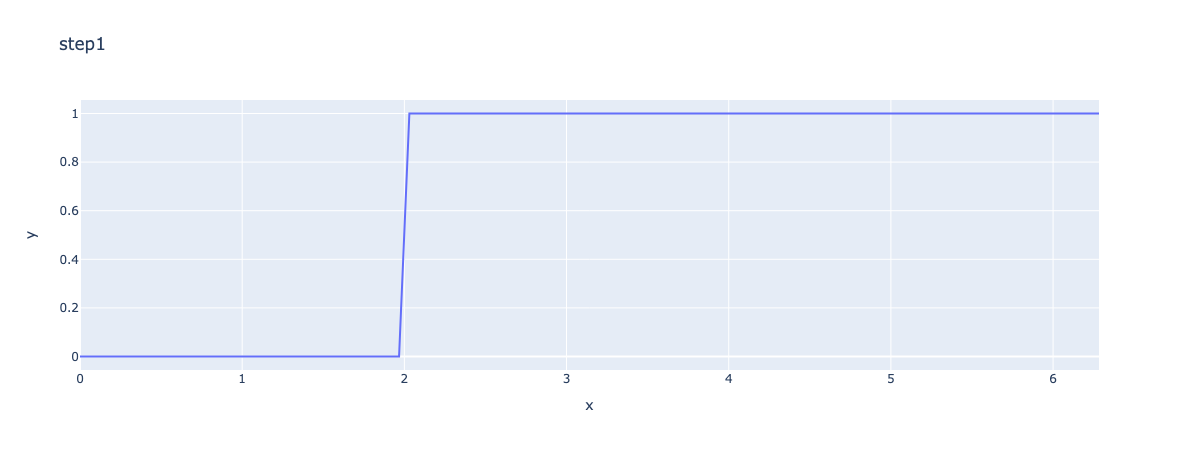
3.4. step1
The function step1 is a step function that is equal to 1 if the argument is greater than 0 and 0 otherwise.
ex=fpp.expr("step1(x,2):x")
x=np.linspace(0,2*math.pi,100)
y=ex.evaluate("x",x)
fig = px.line(x=x, y=y, title="step1",labels={"x":"x","y":r'y'})
fig.show()Results
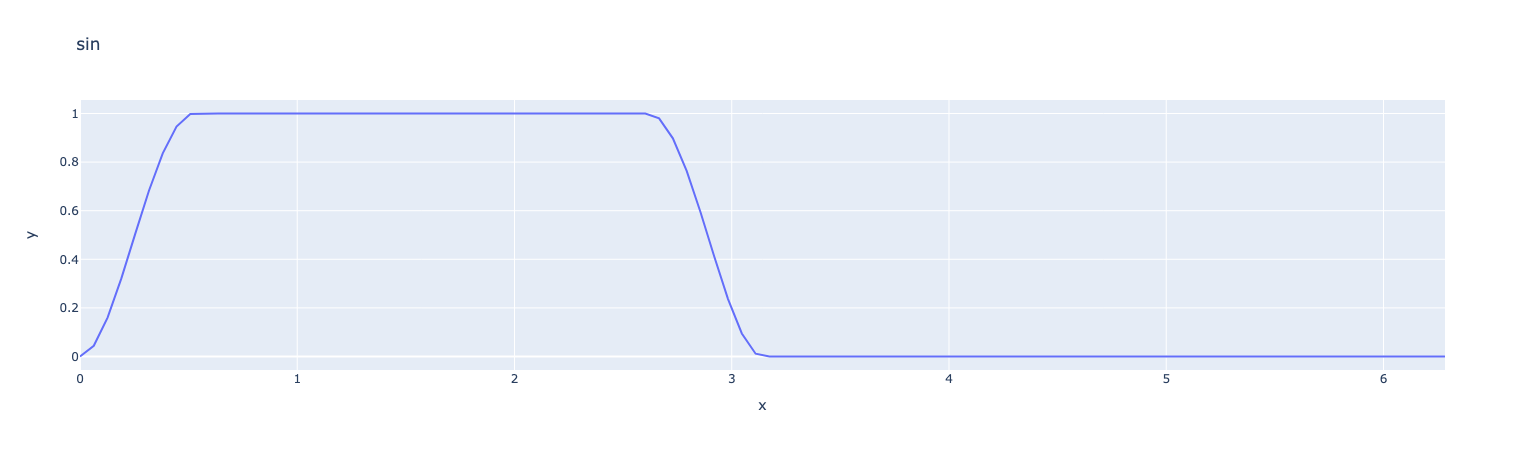
3.5. smoothstep
The smoothstep function is a smooth approximation of the step function.
ex=fpp.expr("smoothstep(sin(x),0,0.5):x")
x=np.linspace(0,2*math.pi,100)
y=ex.evaluate("x",x)
fig = px.line(x=x, y=y, title="smoothstep",labels={"x":"x","y":r'y'})
fig.show()Results
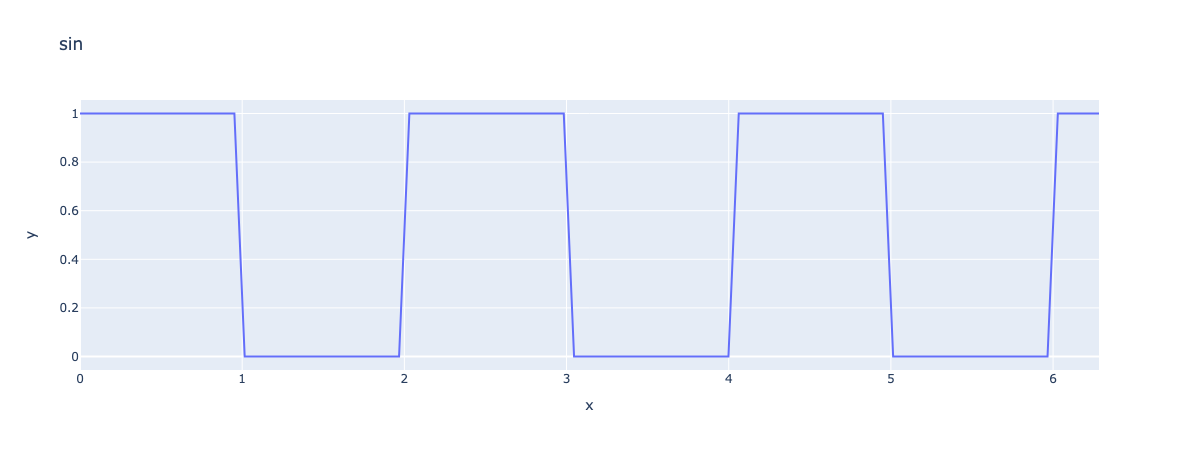
3.6. pulse
The pulse function is defined as \(\text{pulse}(x)=\begin{cases} 1 & \text{if } x\in[0,1] \\ 0 & \text{otherwise} \end{cases}\)
ex=fpp.expr("pulse(x,0,1,2):x")
x=np.linspace(0,2*math.pi,100)
y=ex.evaluate("x",x)
fig = px.line(x=x, y=y, title="rectangle pulse(0,1,2)",labels={"x":"x","y":r'y'})
fig.show()Results
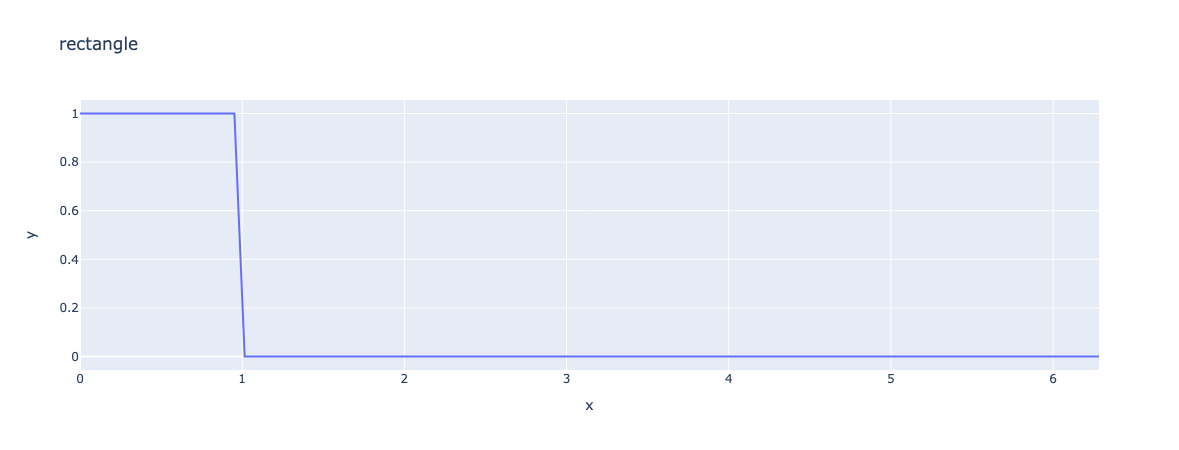
3.7. rectangle
The rectangle function is defined as \(\text{rectangle}(x)=\begin{cases} 1 & \text{if } x\in[0,1] \\ 0 & \text{otherwise} \end{cases}\)
ex=fpp.expr("rectangle(x,0,1):x")
x=np.linspace(0,2*math.pi,100)
y=ex.evaluate("x",x)
fig = px.line(x=x, y=y, title="rectangle rectangle(0,1)",labels={"x":"x","y":r'y'})
fig.show()Results
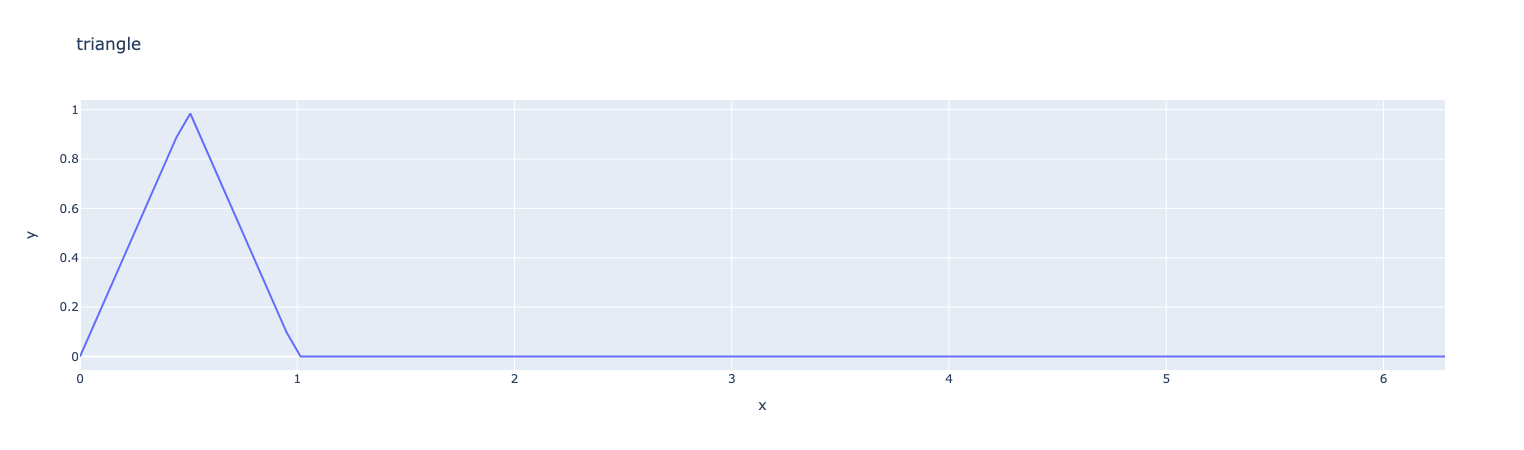
3.8. triangle
The triangle function is defined as \(\text{triangle}(x)=1-\left|\chi_{[a,b]} \left(-1+2\frac{x-a}{b-a} \right) \right\| ], \quad x\in[a,b]\)
ex=fpp.expr("triangle(x,0,1):x")
x=np.linspace(0,2*math.pi,100)
y=ex.evaluate("x",x)
fig = px.line(x=x, y=y, title="rectangle triangle(0,1)",labels={"x":"x","y":r'y'})
fig.show()Results
 .pdf
.pdf
 .ipynb
.ipynb