Theory of Solid Mechanics
1. Notations and units
Notation |
Quantity |
Unit |
\(\boldsymbol{\eta}_s\) |
displacement |
\(m\) |
\(\rho_s\) |
density |
\(kg.m^{-3}\) |
\(\lambda_s\) |
first Lamé coefficients |
\(N.m^{-2}\) |
\(\mu_s\) |
second Lamé coefficients |
\(N.m^{-2}\) |
\(E_s\) |
Young modulus |
\(kg.m^{-1}.s^{-2}\) |
\(\nu_s\) |
Poisson’s ratio |
dimensionless |
\(\boldsymbol{F}_s\) |
deformation gradient |
|
\(\boldsymbol{\Sigma}_s\) |
second Piola-Kirchhoff tensor |
|
\(f_s^t\) |
body force |
-
strain tensor \(\boldsymbol{F}_s = \boldsymbol{I} + \nabla \boldsymbol{\eta}_s\)
-
Cauchy-Green tensor \(\boldsymbol{C}_s = \boldsymbol{F}_s^{T} \boldsymbol{F}_s\)
-
Green-Lagrange tensor
2. Equations
Newton’s second law allows us to define the fundamental equation of solid mechanics, as follows
2.1. Linear elasticity
2.2. Hyperelasticity
2.2.1. Saint-Venant-Kirchhoff
2.2.2. Neo-Hookean
2.3. Axisymmetric reduced model
Here, we are interested in a 1D reduced model, named generalized string.
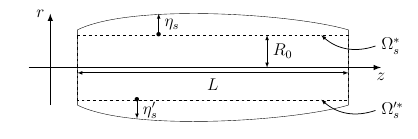
The axisymmetric form, which will interest us here, is a tube of length \(L\) and radius \(R_0\). It is oriented following the \(z\) axis and \(r\) represents the radial axis. The reduced domain, named \(\Omega_s^*\) is represented by the dotted line. So, the radial displacement \(\eta_s\) is calculated in the domain \(\Omega_s^*=\lbrack0,L\rbrack\).
We introduce then \(\Omega_s^{'*}\), where we also need to estimate a radial displacement as before. The unique variance is this displacement direction.
The mathematical problem associated to this reduced model can be described as
where \(\eta_s\) is the radial displacement that satisfies this equation, \(k\) is the Timoshenko’s correction factor, and \(\gamma_v\) is a viscoelasticity parameter. The material is defined by its density \(\rho_s^*\), its Young’s modulus \(E_s\), its Poisson’s ratio \(\nu_s\) and its shear modulus \(G_s\)
In the end, we take \( \eta_s=0\text{ on }\partial\Omega_s^*\) as a boundary condition, which will fix the wall to its extremities.
 .pdf
.pdf