Laminar, Isothermal Backward Facing Step Benchmark
Analysis Type: Separation and reattachment along a backward facing step
| this benchmark has been published by NAFEMS, it has not yet been implemented/tested using Feel++. |
1. Introduction
In a flow system, where the flow cross-section expands too rapidly for the flow to follow, flow separation and subsequent reattachment may occur. There are numerous examples in engineering applications e.g. a wide angle diffuser, a sharp bend, or simply a junction between two channels with different cross-sections. Flow separation is associated with local flow direction reversal that manifests itself in a vortex formation. Such a flow anomaly causes additional pressure losses in the system.
Flow across a backward facing step is one of most studied validation cases in Computational Fluid Dynamics (CFD), mostly because of its simple geometrical arrangement and lack of adequate analytical solution of the flow field. Pressure and flow velocity although strongly coupled do experience significant changes.
2. Objectives
The case of backward facing step tests coupling between the pressure field and the flow velocity. Due to rapid expansion of the flow cross-section, the pressure locally increases, causing flow variations across the channel crosssection, separation and subsequent flow recirculation.
Any modelling deficiency and/or numerical error (e.g. discretization inadequacy, numerical diffusion, equation under-relaxation) inevitably leads to inaccurate prediction of the extent of the recirculation region. Comparing computed velocity profiles and the flow reattachment location with the available experimental data [1], [2] should expose these deficiencies.
3. Geometry
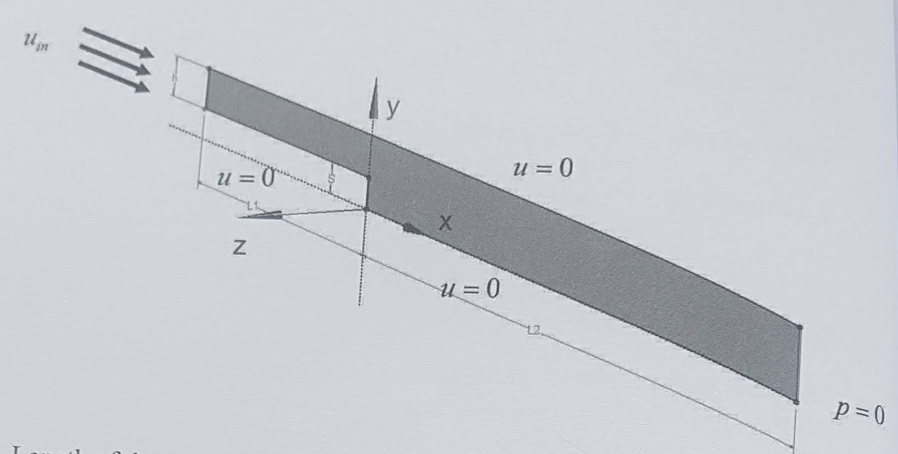
-
Length of the upstream section (L1) is 0.2 \(\mathrm{m}\)
-
Length of the downstream section \((L 2)\) is \(0.5 \mathrm{m}\)
-
Step height (S) is 4.9 \(\mathrm{mm}\) Inlet channel height ( \(\mathrm{h}\) ) is \(5.2 \mathrm{mm}\);
-
Domain width is \(1.0 \mathrm{mm}\) (although not important due to the case twodimensionality).
4. Case Definition
The inflow velocity profile consistent with the laminar flow regime is set at the inlet:
-
\(u_{i n}=6 u_{a v e}\left(\frac{y_{1}}{h}\right)\left(1-\frac{y_{1}}{h}\right) \quad\) where \(y_{1}=y-S\)
-
The friction force and its variation along channel walls further develop the flow profile, and influence its separation and reattachment.
5. Fluid Properties
The fluid properties that correspond to incompressible and isothermal air shall be used: \(\rho\) is density of \(1.23 \mathrm{kg} / \mathrm{m}^{3}\)
\(\mu\) is dynamic viscosity of \(1.79 \cdot 10^{-5} \mathrm{Pa}\) s.
7. Boundary Conditions
-
Velocity profile at the inlet \( u_{i n}=6 u_{a v e}\left(\frac{y_{1}}{h}\right)\left(1-\frac{y_{1}}{h}\right) \text { where } y_{1}=y-s \) and the average velocity ( \(u_{a v e}\) ) are derived from the selected Reynolds number: \(R e=\rho u_{\text {ave}}(2 h) / \mu\) Reynolds numbers of 389 and 1095 are used for the detailed velocity profile comparison. The reattachment length is studied for the range of Reynolds numbers between 100 and 800
-
A no-slip boundary condition \(u=0.0 \mathrm{m} / \mathrm{s}\) is assigned to the bottom and the top wall.
-
For the outlet boundary, a fixed relative pressure (e.g. \(p=0.0 \mathrm{Pa}\) ) is appropriate. The absolute pressure value does not influence the flow velocity results.
-
For the vertical \(X-Y\) surfaces, symmetry or equivalent conditions shall be used.
8. Output
Vertical profiles of the velocity shall be extracted from the CFD simulation results and compared with the experimental data [1]
The diagrams below present two sets of such data for Reynolds number \(\left(\rho u_{\text {ave}} 2 h / \mu\right) 389\) and \(1095,\) respectively. Only a small subset of the experimental data is presented. The coordinate \(x\) represents the downstream distance from the step location and has been normalised with the step height \((S)\)


Another important parameter is the flow reattachment, which is characterised by the change in the flow velocity gradient: \(\partial_{y} u<0 \rightarrow \partial_{y} u>0\)
The reattachment length, which is the distance from the step to the location of the flow direction reversal, shall be calculated and compared to the experimental results \([6.1 \& 6.2\)]

| the reattachment length \(\left(x_{r}\right)\) is normalized with the step height (S). It is presented as a function Reynolds number \(\left(\rho u_{a v e} S / \mu\right)\) that based on the step height ( \(S\) ). |
Data summarises the experimental data in a table form to simplify the validation process. The quadratic mean (or RMS) of deviation can be used to quantify the level of agreement between both sets of results.
Appendix A: Data
A.1. Velocity profiles at \(Re=389\)
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
A.2. Velocity profiles at \(Re=1095\)
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
A.3. Experimental data for reattachment length
\(Re_s\) |
\(x/S\) |
\(Re_s\) |
\(x/S\) |
34.04 |
2.48 |
47.87 |
2.78 |
47.87 |
3.05 |
100.00 |
5.11 |
81.92 |
4.36 |
148.94 |
6.99 |
141.49 |
6.73 |
200.00 |
8.68 |
164.89 |
7.97 |
251.06 |
10.19 |
234.04 |
9.55 |
||
297.87 |
11.47 |
||
References
-
B.F. Armaly, F. Durst, J.C.F. Pereira and B. Schoenung, Experimental and Theoretical Investigation of Backward-Facing Step Flow, J. Fluid Mech., 1983, Vol. 127, pp. 473-496
-
M.K. Denham and M.A. Patrick, Laminar Flow over a DownstreamFacing Step in a Two-Dimensional Flow Channel, Trans. Inst. Chem. Engrs, 1974, Vol. 52, p .361
 .pdf
.pdf